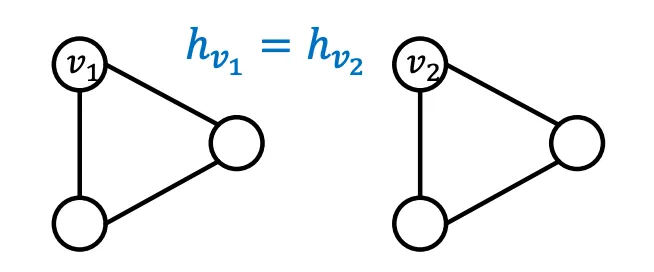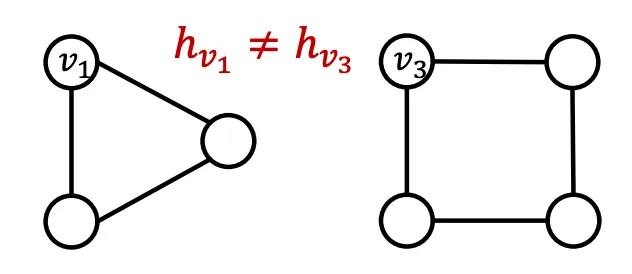예상 독자
•
CS224w 1~15강을 수강했음
•
Message-Passing GNN 및 WL-Kernel에 대해 알고있음
핵심 내용
•
완벽한 GNN의 조건은 무엇이며, 어떻게 도달할 수 있는가 ?
•
Graph에서의 위치를 나타내는 GNN은 어떻게 만들 수 있는가 ?
•
Target Node를 구분하는 ID-GNN은 어떻게 만들 수 있는가?
•
GNN은 Adversarial Attack에 취약한가?
16. Advanced Topics in Graph Neural Networks
이번 강의의 주제는 완벽한 GNN이다. 완벽한 GNN이 무엇이며, 어떻게 동작해야 하는지에 대해 고찰하면서 Adavanced GNN을 만들어 나가는 내용이다.
16.1 How Expressive are Graph Neural Networks
사고 실험을 통해 완벽한 GNN이 어떤 일을 해야하는지 생각해보자. 9강에서도 말 했듯이, 완벽한 GNN이라면 Target Node의 Neighborhood Structure(이하 이웃구조)와 Embedding을 Injective하게 Mapping해야 한다. 이 얘기를 풀어서 설명하면 (1) 같은 이웃구조를 가지고 있는 Node는 같은 Embedding을 가져야하고, (2) 다른 이웃구조를 가지고 있는 Node는 다른 Embedding을 가져야 한다. (Feature는 같다고 가정한다)
이 가정을 바탕으로 “실패"한 모델과 “성공적인” 모델을 정의해보자. 서로 다른 Graph Input (Nodes, Edges, Graphs) 쌍이 들어오면, 실패한 모델은 그 둘을 같은 Embedding으로 매핑할 것이고, 성공적인 모델은 다른 Embedding으로 매핑할 것이다. 이 정의를 기억하며 완벽한 GNN이란 무엇인지 계속 생각해보자. 2가지 조건을 만족시키면 완벽한 GNN일까? 그리고 지금 GNN은 완벽할까?
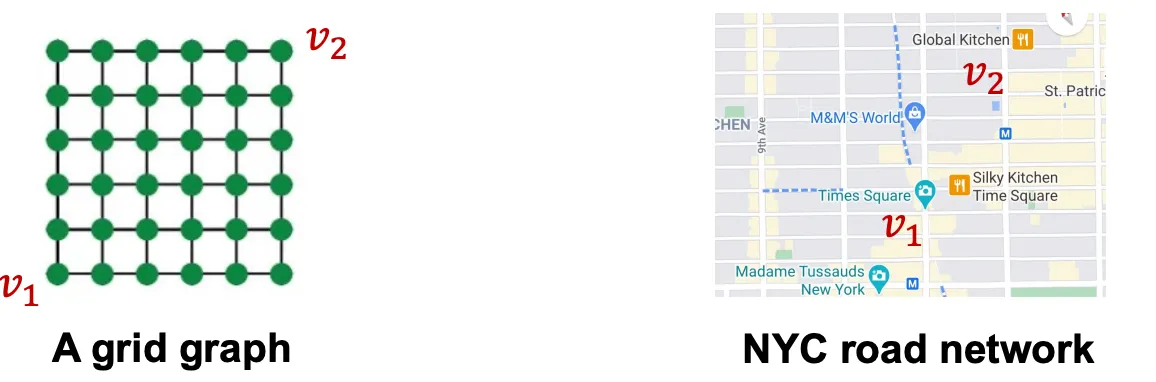
우선 1) 같은 이웃구조를 가진 Node는 같은 Embedding을 가진다는 결함이 있는 조건이다. Graph안에서의 Position이 중요한 정보라면, 같은 이웃 구조더라도, 다른 Position에 놓여있으면 다른 Embedding을 가져야 한다. 이런 경우를 Position-aware Task라고 부르며 (1)을 만족하더라도 Position-Aware Task라면 모델링에 실패했다고 볼 수 있다. 그리고 여태 소개한 GNN중 Position 정보를 Encoding하는 모델은 없다.
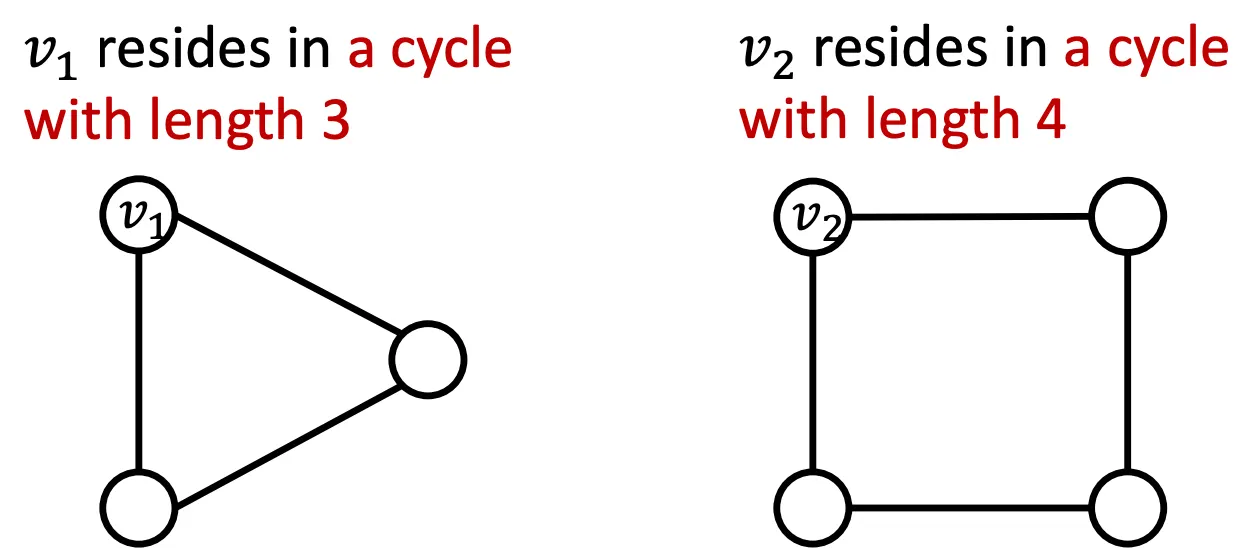
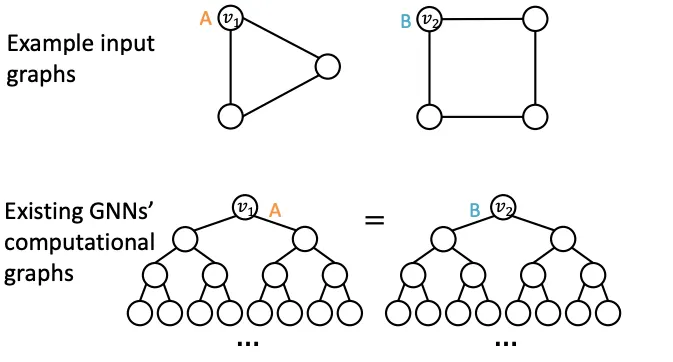
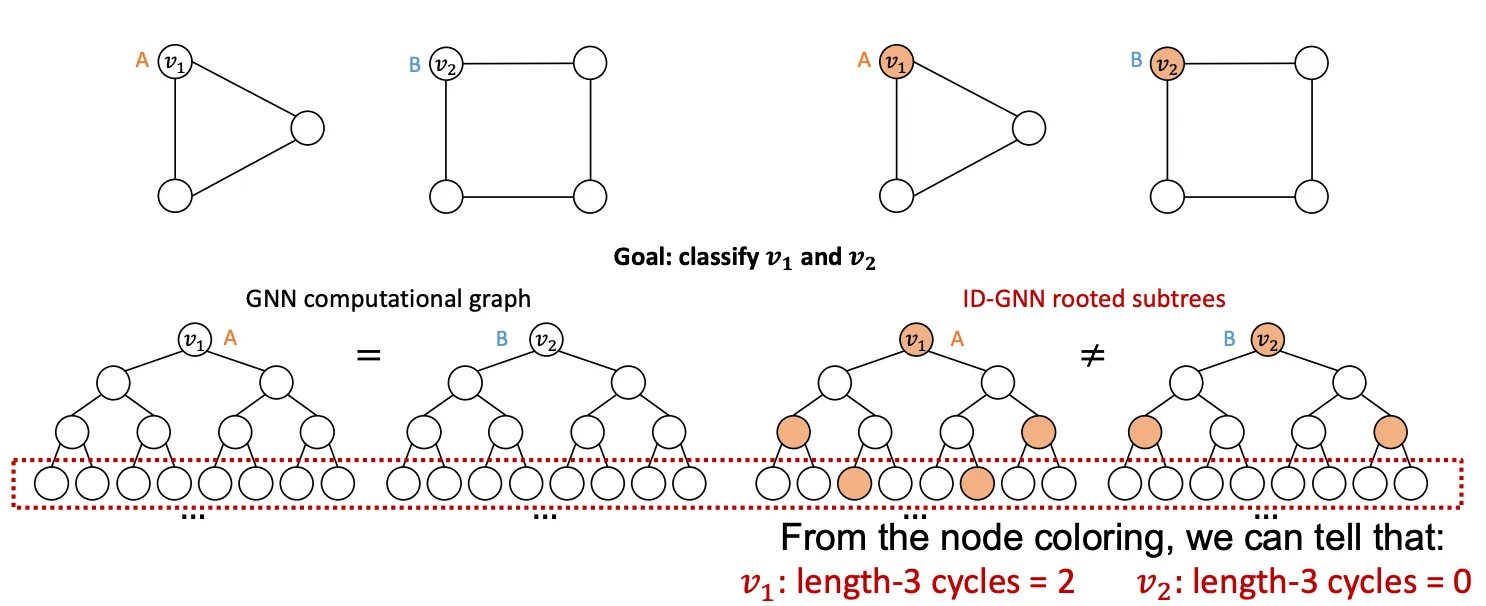
(2) 다른 이웃구조를 가지고 있는 Node는 다른 Embedding을 가져야 한다는 여태 나온 GNN으로 항상 성공할 수 없는 조건이다. Message Passing GNN은 Cycle Count를 전해줄 수 없으므로 아래 예시에서 실패하며, Symetric한 구조에서도 실패한다.
이번 강의에선 이 두가지 문제점을 More Expressive GNN을 설계한다. (1)번 문제는 Graph에서의 Position을 기반으로한 Embedding을 만들어내 해결하고, (2)번 문제는 WL Kernel보다 강력한 Message Passing GNN을 만들어서 해결한다.
16.2 Position-aware Graph Neural Networks
Graph에는 2가지 종류의 Task가 있다. 첫째는 Structural한 역할에 따라 Node의 Label이 정해지는 Structure-Aware Task이고, 둘째는 Graph의 Position에 따라 Label이 정해지는 Postion-Aware Task이다. GNN은 대부분의 Structure-Aware Task를 잘 수행하지만, 아쉽게도 Position 정보는 이용하지 않기 때문에 Position-Aware Task에선 실패한다. 그렇다면 어떻게 해야 GNN이 Position-Aware Task를 수행하게 만들 수 있을까? Anchor 개념이 그 해답이 될 수 있다.
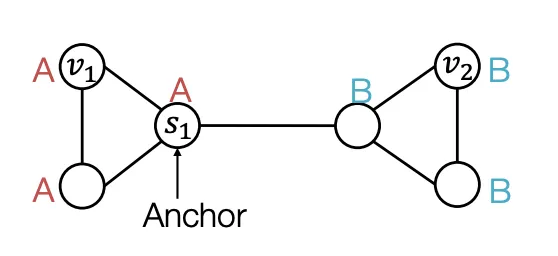
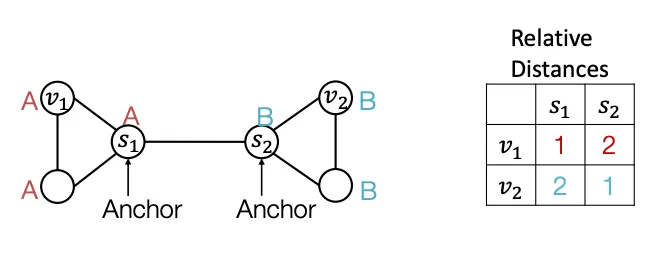
무작위로 Graph의 한 Node를 Anchor로 정했다고 가정해보자() Anchor(Reference Point)가 정해지면 거리를 잴 수 있고, 거리를 잴 수 있다면 위치 정보를 표현할 수 있다. 이때 Anchor Node 하나 당 Coordinate Axis 하나의 역할을 하므로 Anchor Node를 여러 개 사용할 수록 고차원적인 거리 정보를 표현할 수 있다.
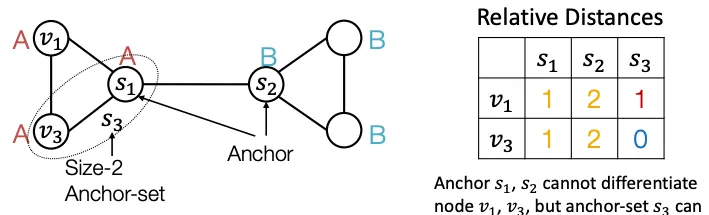
단순히 Anchor Node를 여러개 쓰는것 뿐만 아니라, Set 개념으로 접근하여, Anchor Set에 도달할 수 있는 최소거리 등의 정보를 이용할 수 도 있다. 아래는 , 을 하나의 Anchor Set으로 표현한 예시이다. 여러 사이즈의 Anchor Set을 사용하면 기존보다 효율적으로 Position정보를 인코딩 할 수 있다.
이런 Positional 정보를 어떻게 사용할 수 있을까? 간단하게 생각해 볼 수 있는 방법은 Node의 Feature로 사용하는 것이다.실제로 더욱 풍부한 정보를 주는 것이므로 도움이 많이된다. 주의해야 할 점은 각 인코딩이 무작위 Anchor를 기준으로 정해지므로, 그래프는 그대로인데 정보가 여러 방식으로 인코딩 될 수 있다. 이는 NeuralNet에서 차원 순서가 바뀌는것과 동일한데, 당연히 결과가 크게 바뀔것이다.
이를 해결하기 위한 엄밀한 방식으로는 Permutation-Invariant한 Position Encoding을 만드는 방법이 있다. 다양한 Position-Aware GNN Paper가 이런 방식을 제시하고 있는데 강의에선 다루지 않는다.
16.3 Identity-Aware Graph Neural Networks
전 단원에서 GNN은 대부분의 Structure-Aware Task를 잘 수행한다고 했다. 즉 Structure-Aware Task를 전부 완벽하게 수행하지는 못한다는 뜻이다. Node, Edge, Graph 의 3가지 Level에서 GNN이 풀지못하는 특정Structure-Aware Task를 찾아보자.
실패 사례
1.
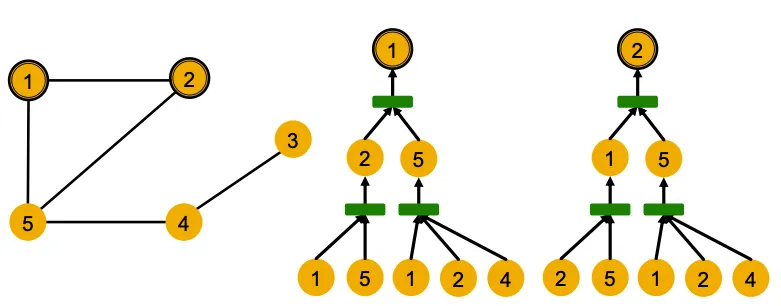
Node Level에서는 다른 입력인데, Compuational Graph가 같은 경우를 예시로 들 수 있다.
2.
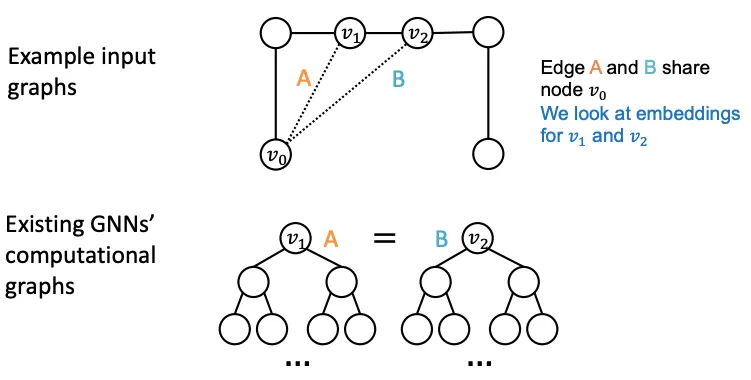
위의 문제는 Edge Level 에서도 동일하게 발생한다. , 의 Embedding이 같으므로, 이 어디에 연결되어야 할 지 알 수 없다.
3.
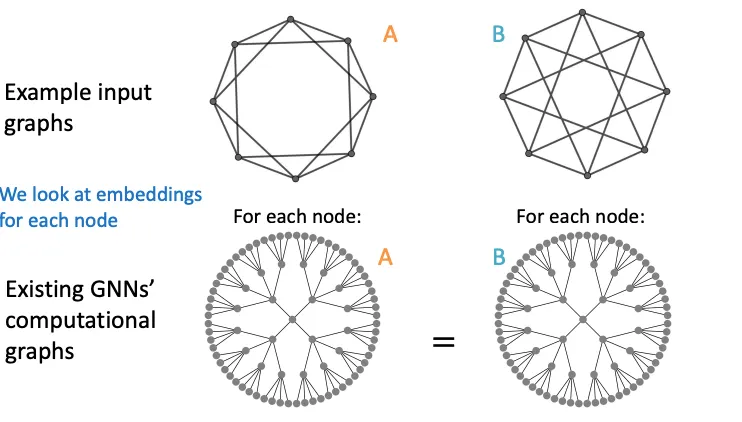
다른 입력을 가지고 있는데, Computational Graph를 그리면 똑같아지는 경우도 있다. 이런 경우 두 Graph는 엄연히 다르지만, 같은 Graph Embedding을 갖게된다.
이 사례들은 자주 발생하지는 않으나, WL-Kernel이나 GNN의 Corner Case로 종종 언급되는 문제이다. 이런 문제는 어떻게 해결해 볼 수 있을까? 이 강의에선 Coloring이라는 방법을 통해 임베딩 하려는 Node에 색상을 할당하는 방식으로 해결한다.
Coloring
여러 Hop에 거친 Computational Graph라면 일반적으로 자기 자신이 포함되는 경우가 잦은데, 이를 이용한 방식이다. Node의 순서와 ID에 Invariant한 특징을 가지고 있으므로, GNN의 특성에도 잘 들어 맞는다. 그럼 Coloring을 이용해 위의 문제를 해결하는 예시를 확인해보자.
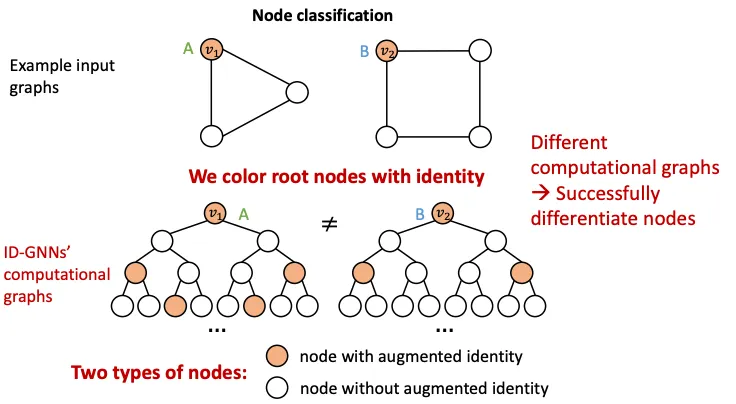
1.
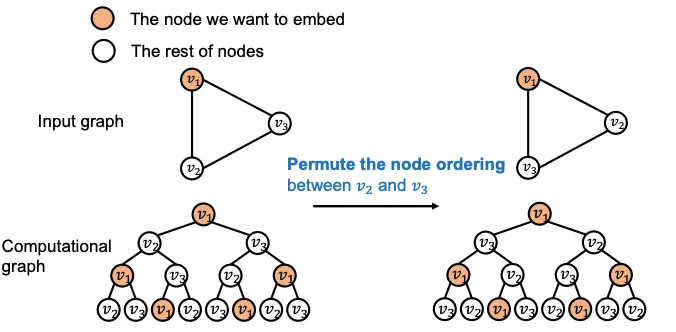
Node Level에서는 다른 입력인데 Compuational Graph가 같은 경우, Coloring을 이용하면 다른 Computational Graph를 갖게되어 Node Classification 문제를 쉽게 해결할 수 있다 !
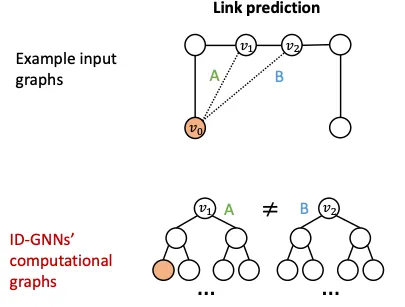
2.
Node Level에서는 다른 입력인데 Compuational Graph가 같은 경우의 Edge Level Task도 관심있는 Node 쌍 중 하나에 대해 Coloring하면, 이 역시 다른 Computaitonal Graph를 갖게되어 문제를 해결할 수 있다.
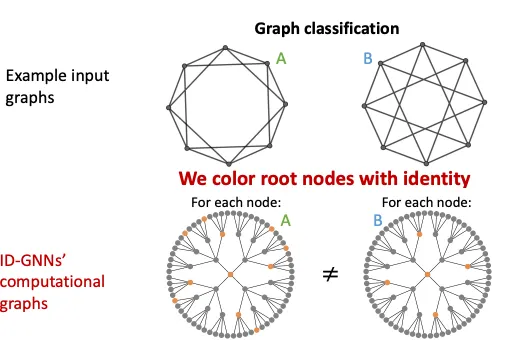
3.
Graph Level도 위에서 말한 사례들과 같은 원리로 풀린다.
ID GNN
시작 Node에 구분할 수 있는 정보를 준다는, 너무나도 직관적인 방식으로 문제를 해결할 수 있음을 확인했다. 그러면 Coloring을 이용하는 GNN은 어떻게 만들 수 있을까? Heterogenous message passing을 이용해 Coloring 개념을 적용할 수 있는데, 이런식으로 Node를 구분하는 GNN을 ID(entity- Aware) GNN (이하 ID-GNN)이라고 부른다.
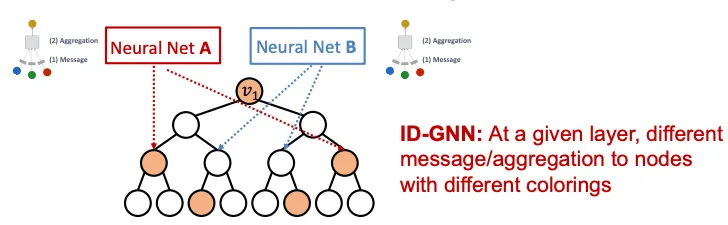
일반적으로 GNN은 모든 Node가 동일한 Message Passing연산을 지닌다. 이와 다르게 ID-GNN은 Heterogenous하게 Message Passing을 수행하는데 문맥에서도 알 수 있듯이, Heterogenous 하다는 뜻은 다른 Node에 다른 Message Passing 연산을 적용한다는 뜻이다.
다시 풀어서 설명하면 Coloring된 Node는 다른 NeuralNet을 통해 Message Passing을 수행한다는 의미인데, 이렇게 다른 Computational Graph를 삽입하면 Coloring을 연산에 녹여낸 것과 같은 개념이므로. 기존에 GNN이 풀 수 없었던 Structure-Aware Task를 풀 수 있게 되는 것이다. 아래는 9강에서 부터 꾸준히 언급해왔던 문제인데, ID-GNN을 이용하면 쉽게 해결할 수 있는 것을 볼 수 있다.
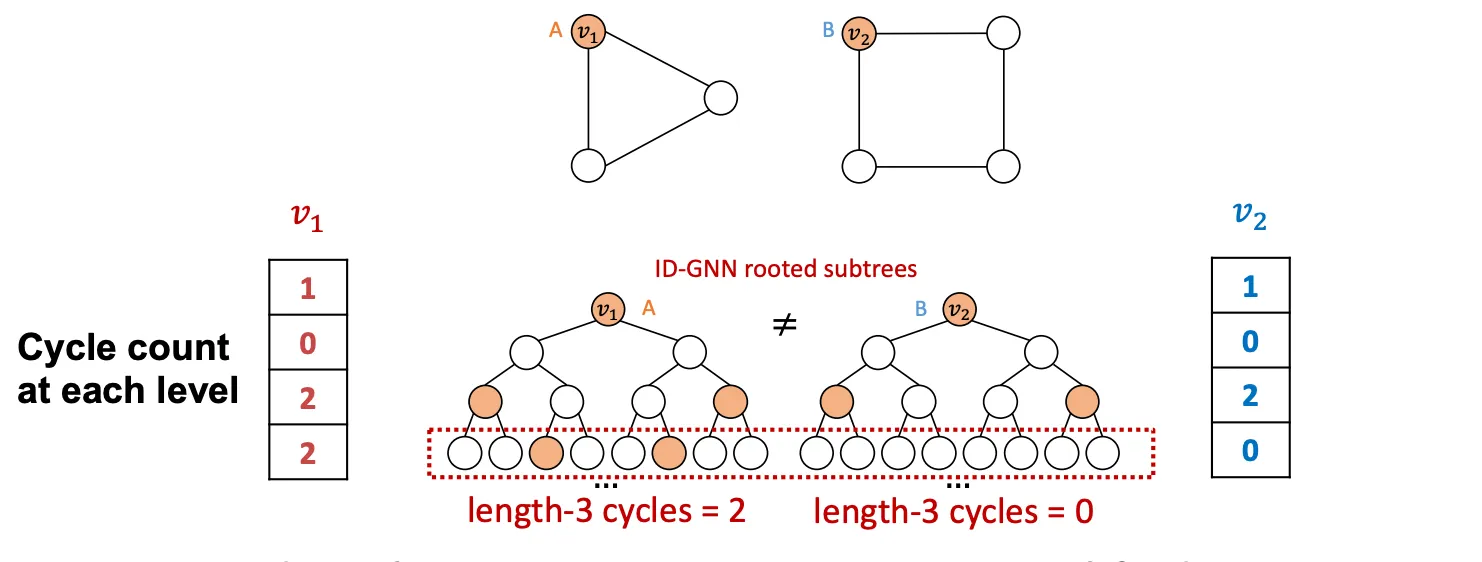
Heterogenous하게 연산을 구성하지 않고, Identity Infomation을 Feature로 추가해주는 방식으로도 어느정도 문제를 해결할 수 있는데 이를 ID-GNN-Fast 라고 부른다. 연산을 여러 종류로 구성하지 않아도 되므로, 비교적 간단하다. Identity Infomation을 인코딩 하기 위해 각 Layer(Hop)의 Cycle Count를 사용하는데, 이 방식은 훨씬 가볍고 어느 GNN과도 함께 쓰일 수 있다.
16.4 Robustness of Graph Neural Networks
(조금 다른 주제)
딥러닝 모델들의 성능이 향상되면서, 다양한 종류의 어플리케이션이 세상에 나오고있다. 이러한 모델들이 세상에 나올 준비가 되어있을까? Adversarial Example을 살펴보면서 딥러닝 모델의 취약점에 대해 이야기해본다.
Adversarial Attack의 가장 대표적인 예시는 CNN와 Noise이다. NeuralNet을 교란시키기 위해 계산된 Noise를 원본 이미지에 더해주면, 육안으로 같은 이미지임에도 불구하고 전혀 다른 결과를 내뱉게 된다. CV Task 뿐만아니라 NLP와 Audio Domain에서도 Adversarial Attack이 가능하다.
Adversarial Attack은 딥러닝 모델이 대개 Robust하지 않다는 점을 보여주는 좋은 예시이다. 이런 취약점은현실세계에서 모델 성능이 예상했던 것 보다 낮게 나올 수도 있으며, 악의적으로 모델을 해킹할 수도 있다는 것을 보여준다.
GNN은 어떨까? 현실세계에서 GNN의 Application은 일반적으로 Public Platform이나, 금전적인 이익을 위해 사용된다.(Ex :RecSys, SNS, Search Engine)즉 현실적으로 GNN의 입력값을 조작하거나, 예측값을 해킹할 충분한 유인이 있다는 뜻이다. GNN은 Adversarial Examples에 대해 Robust할까?
이를 알아보기 위해 현실 세계에서 발생할만한 Adversarial attack의 가능성에 대해 알아보고, (2) 공격하는 입장이 되어 모델을 분석해 본다. (3) Optimization 문제로 수식화 한 뒤, (4) 모델이 얼마나 취약한지를 Empirically 확인한다. 쉬운 설명을 위해 GCN을 이용해 Semi-Supervised Node Classification을 수행한다고 가정하고 얘기한다.
Attack possibilities
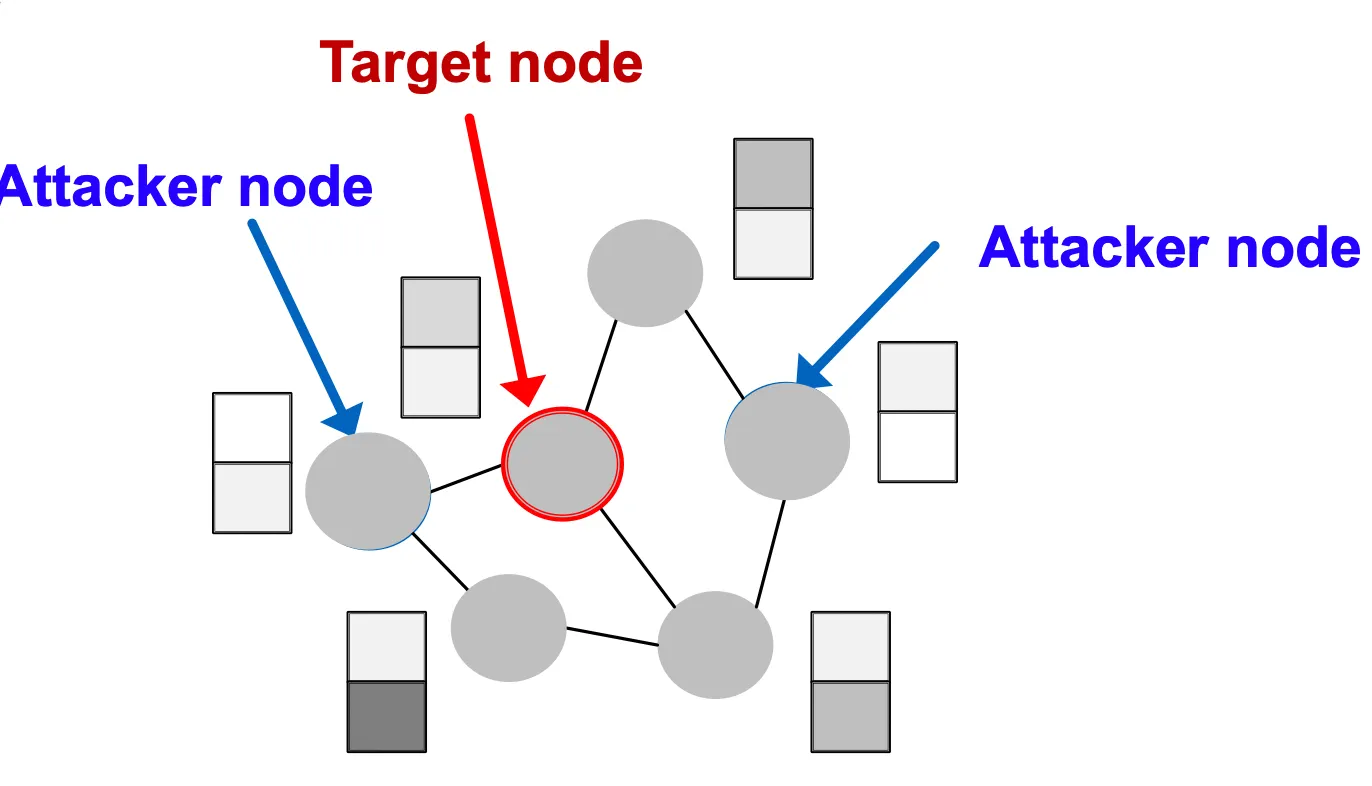
Node의 집합 가 있을 때 공격하고자 하는 Node를 , Attacker 가 수정할수 있는 Node 집합을 라고 해보자. 가 에 포함된다면 Direct Attack, 포함되지 않는다면 Indirect Attack이라고 부른다. 즉 인 경우 Direct Attack이고, 일 경우 Indirect Attack이다.
Attack은 일반적으로 (1) Node의 Feature를 수정하거나, (2) Link를 추가하거나 제거하는 식으로 이루어진다. 예를 들어 (1) 검색 엔진을 공격하기 위해 글 내용 자체, 혹은 연결된 글을 수정하거나 (2) SNS에서 Follower나 Like를 어뷰징하는 사례를 들을 수 있다.
Mathematical Formulation
Attack의 Objective는 Graph의 조작은 최소한으로 하고, Node Label Classification의 변동을 최대한으로 하는것이다. Notation을 이용해 표현하면 다음과 같다.
adjacency matrix, Feature Matrix 일 때 원본 Graph 와 조작한 Graph 는 ≈ 관계에 놓여야 한다. 즉 조작이 알아칠수 없을만큼 작아야 하며,Feature의 분포 등의 변화가 없어야 한다.
이제 를 이용해 GCN으로 Node Label 를 예측한다고 해보자. 이때 로 학습된 Parameter를 , 예측된 Label을 라고 하고, Attacker는 와 배포된 모델을 얻을 수 있으며, 를 이용해 와 를 다르게 만드는것이 목적이다.
기존에 학습된 GCN이 있다면 를 입력해서 학습 시켰을때, 나오는 Label이 있을텐데, ≈ 관계면서 그 Label이 기존 예측 Class로 할당될 확률을 낮추고, 다른 Class로 할당될 확률을 높여야 한다.
이 최적화 문제는 여러 어려운 점들이 있는데 우선 가 Discrete하기 때문에 Gradient 기반 방법론을 적용하기 어렵고, 가 변경될 때 마다 새롭게 학습을 해야한다는 점이다. 최근엔 이 최적화 문제를 조금 쉬운 방법으로 풀 수 있는 많은 근사방법론들이 제안되고 있다.
Experiment
•
Setting :
◦
Semi-supervised node classification with GCN
◦
Graph : Paper citation network (2,800 nodes, 8,000 edges).
◦
Attack type: Edge modification (addition or deletion of edges)
◦
Attack budget on node v: modifications
◦
Random Seed를 5번 바꿔가며 훈련한 결과(5 Times)를 사용
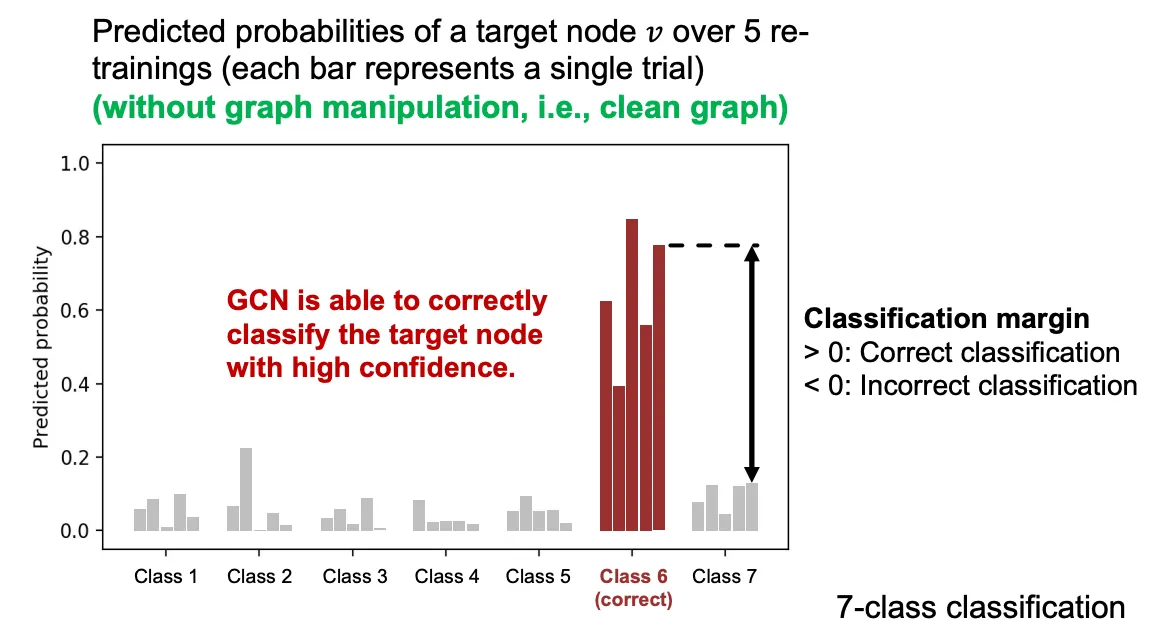
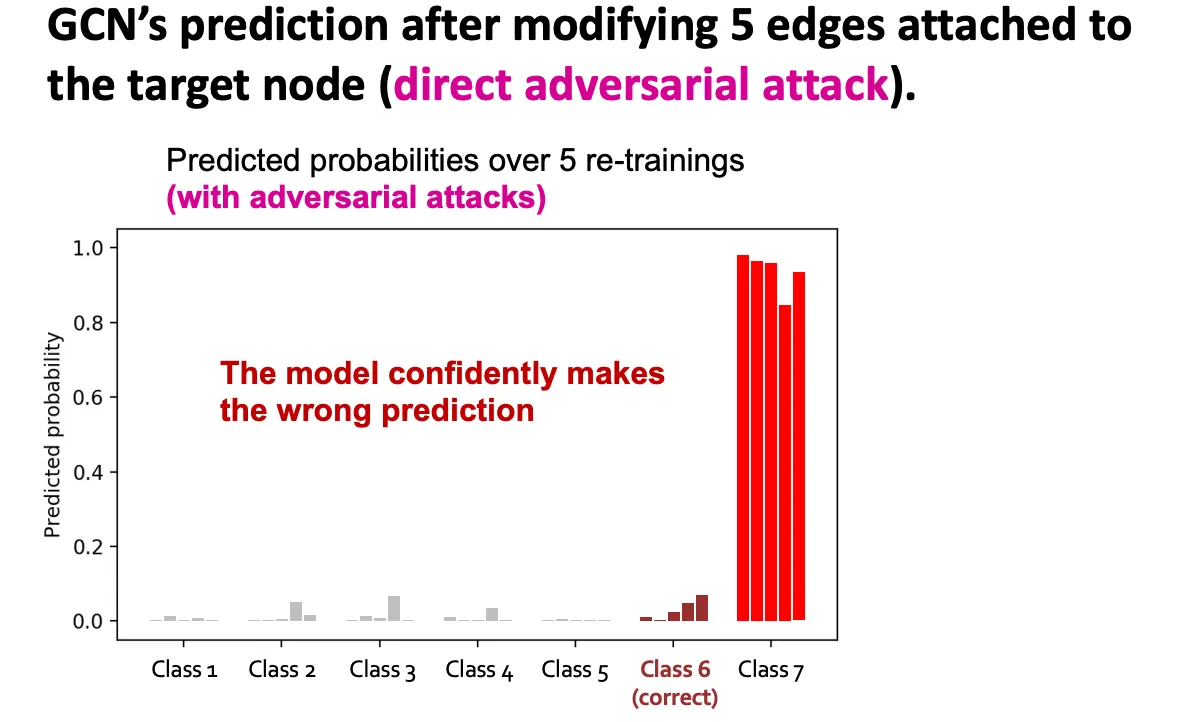
위의 세팅을 기반으로 7-class 분류를 GCN을 통해 5번 진행한 결과가 아래와 같다. 왼쪽 그림은 조작하지 않은 Graph의 결과인데, 5번 모두 Class 6으로 할당된 것을 볼 수 있으며, 다른 Class와의 Margin이 매우 큰 걸 볼 수 있다. 두번째 그림은 5개의 Edge를 Target Node에 붙인 결과인데 예측 양상이 크게 달라진걸 볼 수 있다.
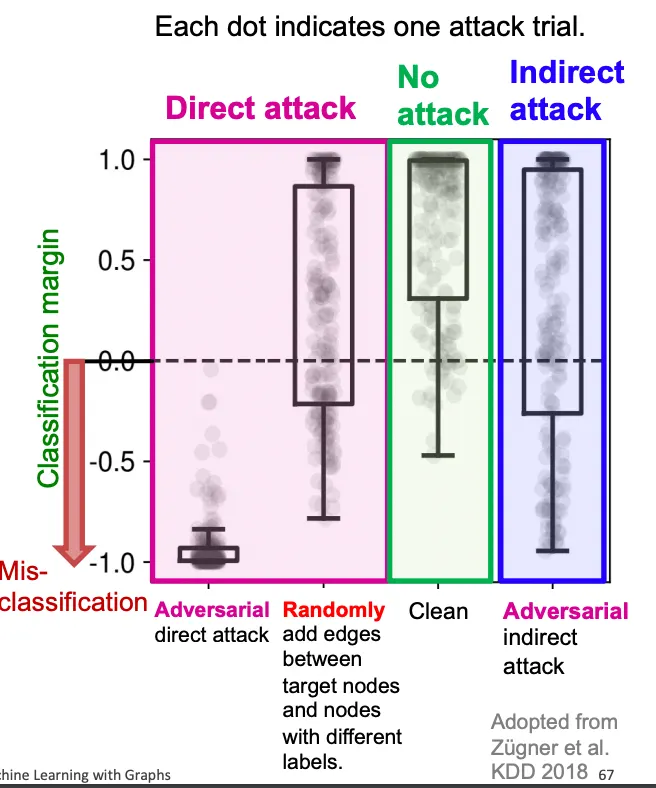
아래는 Attack 방법에 따른 오분류율 시각화인데, Direct Attack은 심각한 영향을 끼치고, Random이나 Indirect는 Attack이라고 하기엔 부족한 모습을 보여주는걸 볼 수 있다.