(GC-MC 리뷰)
Abstract
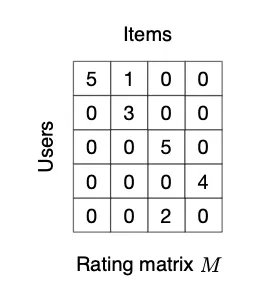
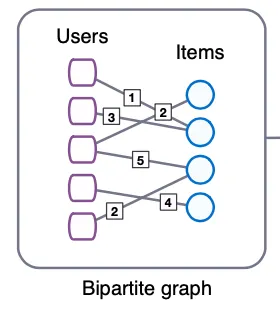
Graph Convolutional Matrix Completion(이하 GCMC)은 Matrix Completion 문제를 Graph간의 Link Prediction으로 풀어낸 방법이다. 예를들어 유저가 영화에 평점을 매긴 Interaction Data가 있다고 생각해보자. Graph 관점에서 이 데이터를 바라보면, 유저와 영화 두 타입의 Node가 존재하는 Bipartite Graph이며 평점은 Edge라고 생각할 수 있다.
GCMC는 Bipartite Interaction Graph에 대해 미분 가능한 Message Passing을 수행하는 AutoEndoer 기반의 모델이다. 일반적인 Collaborative Filtering BenchMark를 상회하는 성능을 보이며, Social Network같이 구조적인 정보나 Feature가 풍부한 세팅 아래에선 SOTA를 상회하는 성능을 보인다.
Introduction
추천 시스템(RecSys)은 크게 Contents-Based, Collaborative Filtering 2가지 종류로 구분될 수 있다. Contents-Based 추천시스템은 Rating이나 전환(구매) 여부를 예측하기 위해 유저와 아이템의 정보를 사용하는 방식이다. Collaborative Filtering은 Interaction Data를 이용해 User-Item간의 Matrix를 만들어, 빈 곳을 채우는 방식이다.(Matrix Completion이라고 불린다)
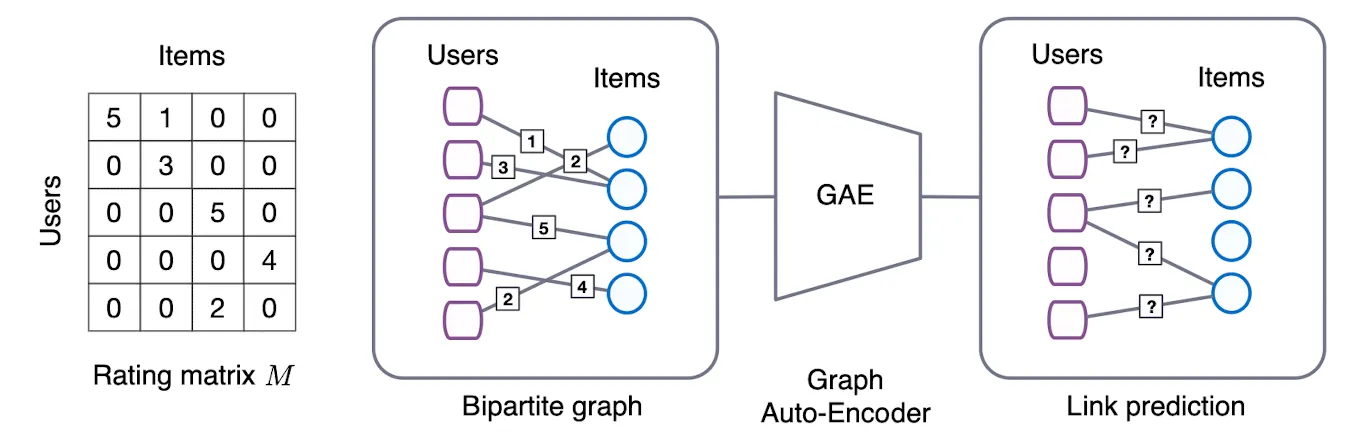
GC-MC는 Interaction Data를 User와 Item의 Bipartite Graph로 나타내어 Matrix Completion Task를 Link의 Label을 예측하는 Task로 재정의한 연구이다. 최근 눈부신 성과를 보이고 있는 GNN을 활용함으로서 Latent Feature를 효과적으로 만들어 내고, 외부 정보를 쉽게 결합할 수 있는 구조를 만들어 냈다. 특히 Side-Information을 이용해, Cold-Start 관련 성능 Bottleneck을 어느정도 완화할 수 있음을 실험을 통해 증명했다.
Method
Rating Matrix와 Matrix Completion
User , Item 가 있을때, Rating Matrix 은 로 표현될 수 있다. 이때 의 각 원소는 관측된 Rating 혹은 관측되지 않음(0)으로 채워진다. Matrix Completion은 0으로 채워진 부분을 예측하는 Task라고 볼 수 있다.
Link Prediction Notation
Interaction Data를 Graph 관점에서 보면 Undirected Graph 로 나타낼 수 있다.
(이때 는 Node의 집합, 는 Edge의 집합, 은 Edge의 Label 집합을 나타내는 Notation이다.)
는 User와 Item의 합집합 () 으로 볼 수 있고 은 평점의 종류() 라고 볼 수 있다. 그리고 는 User와 Item간의 연결, 즉 라고 볼 수 있다.
선행 연구들
추천시스템에 Graph 방법론을 적용하는 선행 연구들은 Graph Feature Extraction과 Link Prediction Model을 따로 훈련시키는 Multi-Stage 방법론을 채용했다. 그러나 최근 여러 연구가 다양한 테크닉을 이용해 Graph를 End-to-End로 학습시켜 획기적인 성능향상을 보이고 있으며, 특히 Auto-Encoder를 이용해서 Unsupervised Learning과 Link Prediction을 하기도 하는데, GC-MC는 그러한 연구의 일종이다.
Graph Auto-Encoder
기본 구조
Graph AutoEncoder도 일반적인 AutoEncoder와 같이 Encoder-Decoder 구조로 이루어져 있다.
( : Node 수, : Feature 차원, : 임베딩 차원, : 인접행렬(Adjacency Matrix)을 의미한다)
Encoder는 Feature , 인접행렬 를 입력받아, Node Embedding 를 만들어 내는 역할을 하며 위의 수식에서 와 같다.
Decoder는 Node Embedding 쌍()을 입력 받아, 인접행렬의 원소 를 예측하는 역할을 하며, 위의 수식에서 와 같다.
Bipartite Recommender Graph 구조
Graph AutEncoder를 Bipartite Recommender Graph에 적용한 수식은 다음과 같다.
( :User 임베딩, : Item 임베딩, : 평점 의 인접행렬을 의미한다.)
Encoder는 Feature 와 Binary 인접행렬 을 입력받아 Node Embedding 를 만들어 낸다.
Decoder는 Embedding 쌍을 받아 Rating Matrix 을 다시 만들어 낸다. 이렇게 만들어진 과 Ground Truth 을 비교해 Reconsturction Error가 최소화 되도록 Auto-Encoder를 학습시킨다.
Graph Convolutional Encoder
Graph Encoder는 Local Graph Covolution Layer에서 영감을 받아, Edge 유형별로 채널을 분리하여 효율적으로 Weigth Sharing을 한다.
Local Graph-Convolution
Local Graph Covolutin은 일종의 Message Passing 연산이다. Message Passing이란 Graph의 Edge를 타고 돌아다니며 Node끼리 Vector 형태의 Message를 주고 받는 것인데, 수식으로는 다음과 같이 표현될 수 있다.
각각의 요소를 분해해서 수식을 이해해보자.
•
는 Item 와 User 가 관계에 놓여있을때 Item에서 User 방향으로 Message Passing을 하는 상황이다.
•
는 Normalization을 위한 상수이며 Node의 Degree를 이용하는데, 메세지를 받는 쪽의 Degree (로 나눠주거나, 두 Node의 Degree를 다 사용하기도 한다()
•
은 Edge의 Type 마다 존재하는 가중치 행렬이고, 는 각 Node의 Feature Vector이다.
위의 수식을 통해 Edge Type 마다 연결된 모든 Node에서 Message Passing을 받으면, Accumulation(Aggregation)을 수행한다. Message Passing과 Accumulation을 수행하는 Layer를 합쳐서 Graph-Convolution Layer로 부르며 수식으로는 다음과 같이 표현될 수 있다.
•
은 Accumulation 연산을 의미하며, Concat이나 Sum으로 구현될 수 있다.
•
은 Element-Wise activation Function을 의미하며 Relu등으로 구현될 수 있다.
위의 수식을 통해 를 구했으면 가중치 Matrix 와 Activation Function을 이용해 최종 Embedding을 만든다. 이 Layer를 Dense Layer로 부르며 수식으로 표현하면 다음과 같다.
Item Node 에 대한 Embedding도 같은 방식으로 이루어지는데, 추가적인 Feature로 Side Infomation을 사용한다면 를 Node Type별로 구성해주어야 한다. 더 깊게 쌓거나, Message Passing에 Attention을 추가할 수 있는데 지금 설명한 방식이 가장 효율적이다.
Bilinear decoder
Encoder가 Item와 User를 Embedding하는 역할을 한다면, Decoder는 Embedding 쌍을 입력받아 Rating Matrix를 Reconsturction하는 역할을 한다. GC-MC에선 각 Rating에 속할 확률을 가중 평균을 내서 구한다. 각 Rating에 속할 확률은 Softmax의 변형을 통해 구해지는데 수식은 다음과 같다.
일반적인 Softmax에 와 Embedding Vector를 곱해주는 형태로 볼 수 있는데, 는 Shape을 가진 Trainable Weight이다.
각 확률을 구했으면, Rating과 Rating에 속할 확률을 곱해서 합한 값 (기대값)을 Reconstructed Rating 로 사용한다. 이 과정을 수식으로 다시 정리하면 다음과 같다.
Model Training
Loss Function은 일반적인 Negative Log Likelihood(Cross Entropy)를 사용하는데, 관측되지 않은 Rating에 대해 Loss를 발생시키지 않기 위해 Masking을 사용한다.
•
은 인 원소들만 1의 값을 갖고, 나머지 원소는 0의 값을 갖음을 의미한다.
•
는 관측된 Rating을 1, 아닌 경우를 0으로 마스킹하는 Matrix이다.
수식을 풀어서 해석하면 (1) 관측값이 있는 Interaction에 대해 (2) Interaction의 Rating Class별로 추정한 확률값에 대해 Cross Entropy를 구하고 (3) 다 합해서 Loss로 사용한다 !
Node Dropout
학습된 모델이 관측되지 않은 Rating에도 잘 동작하게 만들기 위해서, Denosing Setup을 추가해 준다. 특정 Node의 모든 Outgoing Message를 끊어버리는 방식으로 Node Dropout이라고 불린다. 이때 Convolution의 Regularization Scalar는 Dropout이후 다시 구해진다.
특정 Outgoing Message에 대하여 Dropout하는 Message Dropout 방식도 있는데 Node Dropout이 더 효율적임을 실험을 통해 알아냈다. Hidden Layer Unit에는 일반적인 Dropout을 적용하였다.
Mini Batching
거대한 Graph에 대해서는 모든 Node와 Rating Type을 한번에 고려하기 어렵기 때문에 Sampling을 통해 학습시킨다. 일종의 Mini-Batch 개념인데, Memory도 효율적으로 사용하면서 Regularization 효과도 기대할 수 있다. 다만 Full-Batching이 가능한 그래프에 대해서는 Full-Batch가 수렴속도가 더 빨라 Full-Batch 방법으로 학습시켰다.
Vectorized Implementation
구현시에는, 효율적으로 Sparse Matrix를 연산하기 위해 (Norm) 등을 행렬째로 연산한다.
Input Feature Representation and Side Information
각 Node에 대한 Information Feature가 있다면, Input Feature Matrix 로 사용해 Graph Encoder에 바로 넣어줄 수 있다. 그런데 이 Feature가 각 Node를 구분하기에 충분치 못한 정보라면, Graph Convolution 과정에서 오히려 정보 병목이 발생할 수 있다.
이럴 땐 Dense Layer에서 Side Information으로 Feature를 넣어주는 방법을 고려해 볼 수 있다. Node 의 Feature를 Side Information으로 넣어주는 수식은 다음과 같다.
Conclusion
GC-MC는 Recsys의 Matirx Completion Task를 Graph AutoEncoder를 이용해 푸는 접근방식을 제시했다. Encoder는 Graph Convolution을 이용해 User, Item 임베딩을 만들어 내고 Decoder는 임베딩 쌍을 받아 평점의 Class를 예측한다.
GC-MC의 Graph AutoEncoder 구조에는 User, Item의 Side Information을 쉽게 넣어줄 수 있으며 Interaction Data와 Side Information을 둘 다 사용할 수 있는 BenchMark에 대하여 SOTA급 성능을 보여준다.
향후 연구에서는 RNN이나 CNN을 이용해 Multi-Model Side Information을 이용할 수 있도록 확장하거나, Local Neighborhood를 Sampling해서 더 큰 Graph에 대해 Task를 확장하는 방향이 있을 것으로 보인다.