Linear Regression Model
(는 예측값, 는 Weight(Parameter))
선형 회귀 모델은 일반적으로 가중치(Weight)와 Bias로 이루어져 있으며, 입력 Feature의 가중치 합과 Bias를 더해 Prediction을 만들어 낸다. 위는 선형 모델의 일반적인 형태이다.
Fitting
Fitting은 Model이 Train Set을 가장 잘 맞추도록 Parameter를 설정하는 것이다. 일반적으로 선형 회귀 모델에서 사용되는 Metric은 RMSE므로, 선형 회귀 모델을 Fitting 한다는 것은 곧 Train Set의 RMSE를 최소화하는 Parameter()를 찾는다는 것이다.
Method 1 : Nomral Equation
를 찾기 위한 해석적 방법이 있으며 이를 정규방정식(Noraml Equation)이라고 한다. 정규 방적식의 식은 위와 같다. 정규방정식은 의 역행렬을 개산해야 하는데, 이때의 계산복잡도는 ~ 사이에 존재한다(n은 Feature의 갯수). 따라서 이 방법은 큰 데이터셋에 대해 적용하기 힘들다.
Method 2 : Gradient Descent
Gradient Descent는 다양한 문제에서 최적의 답을 찾을 수 있는 Optimization Method이다. 가장 기본적인 아이디어는 Cost를 최소화 하기 위해 반복적으로 피팅(Iterative Fitting)을 해나가는 것이다.
함수의 전체적인 형태를 잘 모르거나, 복잡한 형태여도 그때의 Gradient에 의존하므로 어느정도 해를 잘 찾아갈 수 있으며, 컴퓨터로 쉽게 구현할 수 있으며, 비교적 효율적이라는 장점을 갖고 있다.
Gradient Descent를 설명하기 위해 자주 인용되는 예시는 산에서 길을 잃은 채로 내려가는 상황이다. 길을 모를때 빠르게 산을 내려가기 위한 직관적인 방법은 가장 가파른 길(기울기)을 따라 바닥에 도착할 때 까지 계속 아래로 내려가는 것이다. 이때 기울기가 Cost 함수에 대한 의 Gradient이다. 구체적으로 설명하면 다음과 같다.
1.
임의의 초기 을 설정하고
2.
에 대해 미분을해 Cost 함수의 Gradient를 구한다.
3.
Cost가 감소하는 방향으로 이동한다
4.
2,3번을 만족스러울 때 까지 반복한다
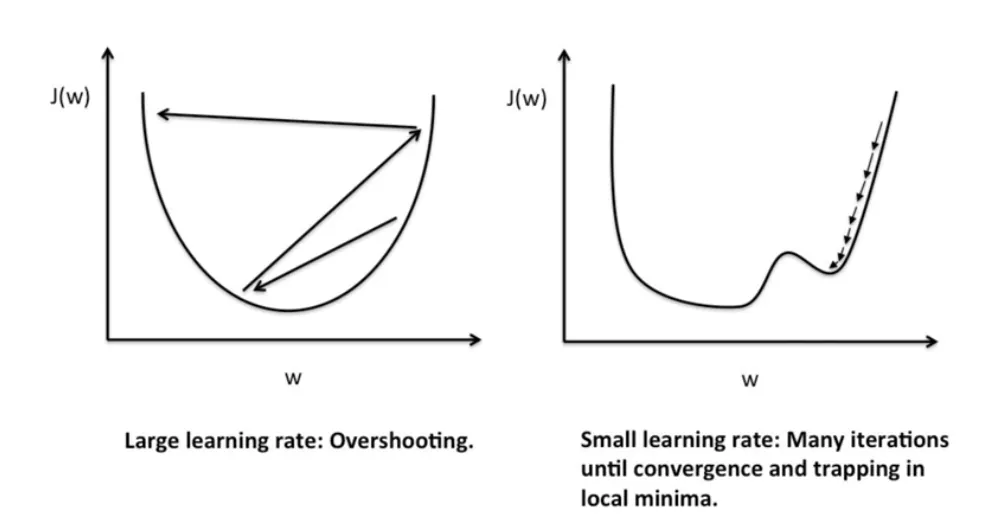
이때 중요한건 한 번 이동할때의 Step 크기다. 학습률(Learning Rate)로 표현되는 이 파라미터는
(1) 너무 크면 (예시가 직관적이지만) 바닥을 지나가 버리기 때문에 아예 내려가지 못할 수 있으며
(2) 너무 작으면 내려가는데 오래걸리고, 평탄한 지역을 바닥으로 착각해 진짜 바닥에 도착하지 못할 수 있다.
Batch Graident Descent
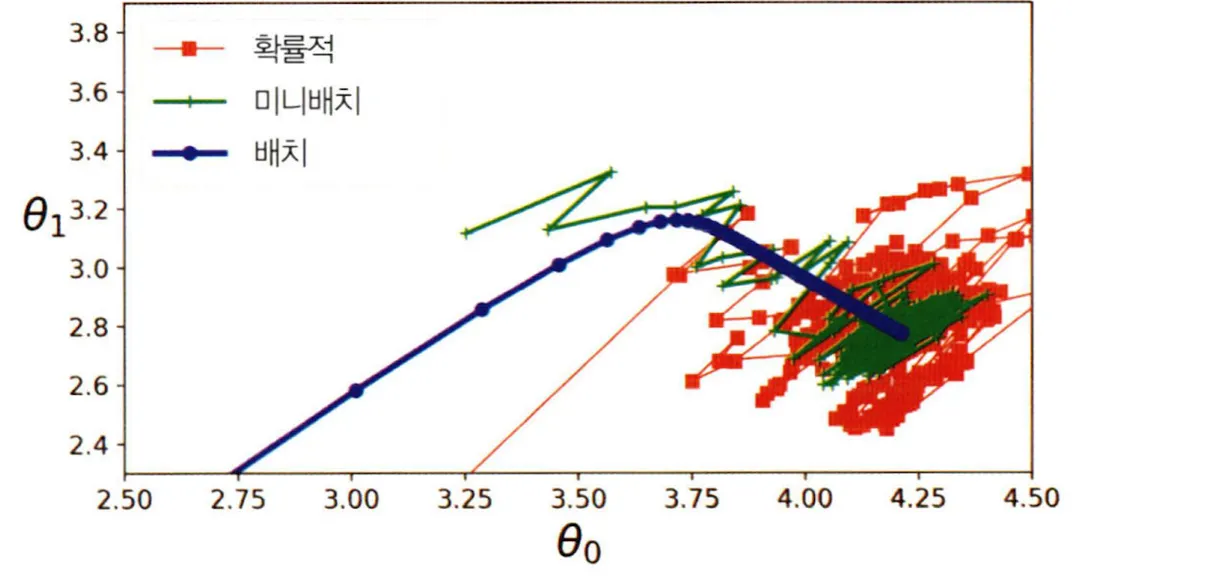
Gradient를 (1) 전체 Dataset에 대해 구하면 Batch Graident Descent (2) 한 개의 Sample에 대하여 구하면 Stochastic Gradient Descent (3) Subset(n>1) 에 대하여 구하면 Mini Batch Gradient Descent 로 분류할 수 있다.
1.
Batch Gradient Descent 는 Dataset을 대표하는 Gradient를 구할 수 있으나, 큰 Dataset에서는 연산량이 매우 크고 느리기 때문에, 딥러닝에서 자주 쓰이지 않는다.
2.
Stochastic Gradient Descent(SGD)는 하나의 Sample로 부터 Gradient를 구하므로 훨씬 빠르지만 Gradient가 굉장히 불안정하다. 이 특성이 평탄한 지역(Local MInimum)을 벗어나는데 도움을 주지만, 동시에 수렴도 어렵게 만든다.
3.
Mini Batch Gradient Descent는 Sample Set를 가지고 Gradient를 구해 비교적 안정적이고, GPU를 통해 병렬적으로 처리할 수 있는 한도 내에서 아주 빠르다. 일반적으로 Batch 단위 학습이라고 하면 이것을 가르키며, 광범위하게 사용된다.
출처 : 핸즈온머신러닝