Graph의 Node를 저차원으로 임베딩하는 방법이 다양한 Prediction Task에서 효과적이라는 것이 여러 실험을 통해 입증되었다. 그러나 당시 방법론들은 근본적으로 Transductive 하다는 문제를 안고있었다. 이는 모델이 학습시 등장하지 않았던(이하 Unseen) Node 에 대하여 예측을 잘 수행할 수 없다는 뜻인데, 현실에서 대부분의 Graph가 계속해서 확장되는 것을 생각해보면 Transductive 방법론은 한계가 자명하다. (* 계속 확장되는 Graph를 Evolving Graph라고 부름)

저자들은 이를 지적하며, Node Feature를 이용해 Inductive한 예측이 가능한 모델 구조(GraphSAGE)를 제시한다. GraphSAGE는 각 Node의 Embedding을 학습시키는 대신, Node의 이웃들로부터 정보를 수집하는 방법을 학습시킨다.

이를 통해 Evolving Graph & Unseen Node에 대해 강력한 예측 성능을 보이는 Inductvie Framework를 만들었다.

Introduction

Previous work

기존 연구들은 Sparse & Wide Node Embedding을 Dense & Low Dimension Embedding으로 Projection하는데에 집중했다. 이렇게 얻어진 Node Embedding은 DownStream Task에서도 강력한 성능을 보이며 그 유용성을 입증해냈다.

Transductive Framework

현실에서의 Graph Data를 생각해보면 계속해서 Node가 추가되거나 없던 Link가 생겨난다. (Ex: Reddit, Youtube, Citation) 즉 현실의 문제를 풀고싶다면, Unseen Node에 대해서도 좋은 Embedding을 추출해 낼 수 있어야 한다.

그러나 대부분의 기존 연구들은 Matrix Factorization 기반의 Transductvie한 접근 방식을 채택했다. 이는 고정된 Graph로 부터 Node를 잘 Embedding하는 문제에 집중했다는 뜻인데, 이는 Evolving Graph의 문제를 풀기에 적합한 구조가 아니다.

GraphSAGE : Inductive Framework

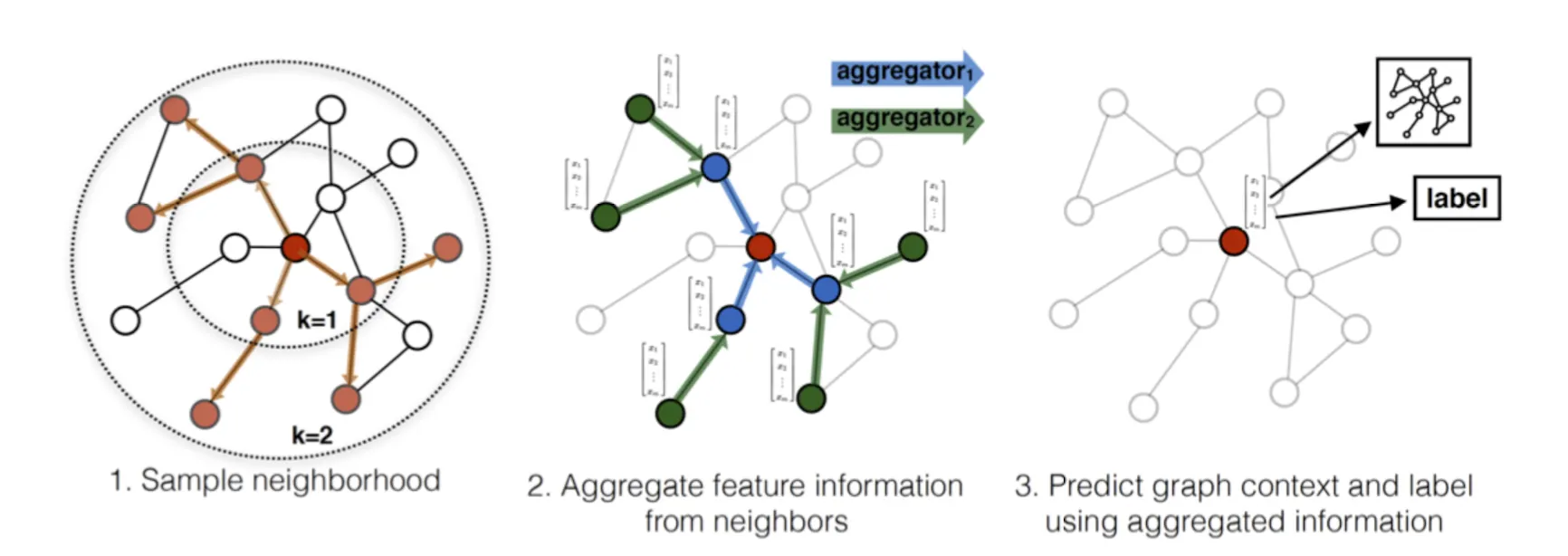
저자는 위의 문제를 지적하며 Inductive한 Node Embedding Frameworkd인 GraphSAGE(SAmple and aggreGatE)를 제시한다. GraphSAGE는 Unseen Node에 대해 일반화 가능한 Embedding Function을 만들기 위해 Node Feature를 적극적으로 사용한다. Node Feature를 사용함으로서 Topological 정보 자체와, 주변 Node들의 Feature 분포 정보를 이용하는 방법을 학습한다.

GraphSAGE는 각 Node를 바로 Embedding하는 대신, 이웃 Node로 부터 정보를 Aggregate하는 함수를 훈련시킨다. 구체적으로는, 취합 함수

Aggregator_k

을 이용해 관심 있는 Node로 부터

k

Hop 만큼 떨어진 이웃들의 정보를 취합하는 방법을 학습한다. 이때 용도에 따라 Unsupervised Loss를 이용해 학습시킬 수도 있고, Task-Specific한 Supervision Loss를 이용해 학습시킬 수도 있다.

Method : GraphSAGE

GraphSAGE의 핵심은 결국 Node의 (가까운)이웃들로 부터 Feature Information을 Aggregate 방법을 배우는것이다. 설명을 위해 학습을 마친 Aggregator들을 이용해 Embedding을 만드는 것(Forward)먼저 설명하고, 이를 최적화하는 방식(Back)을 설명한다.

Notation

•

KKK : Search Depth(Hop)를 의미한다. 얼마나 떨어져 있는 이웃의 정보까지 Aggregate하는지 결정한다.

◦

k∈{1,...,K}k \in \{1,...,K\}k∈{1,...,K}

•

V\mathcal{V}V : 전체 Node의 집합을 의미한다. 각 Node는 vvv로 Notation되며, v∈Vv \in \mathcal{V}v∈V 이다.

•

Wk\bold{W}^kWk: kkk-Hop의 Aggregator의 가중치를 의미한다.

•

xvx_vxv​ : Node vvv의 Feature이다.

•

N(v)\mathcal{N}(v)N(v) : Node vvv의 1-Hop 이웃 집합을 의미한다. 

•

zvz_vzv​ : Node uuu의 Vector Representation, 즉 Embedding Vector를 의미한다.

Embedding Generation : Forward Propagation

학습을 마친 Aggregator들을 이용해 모든

v

에 대하여 Vector Representation을 뽑는 예시를 통해 설명한다.

전체 그래프

\mathcal{G} = ( \mathcal{V},\mathcal{E} )

와 모든

v

에 대하여

x_{v}

가 주어졌을때, 다음과 같은 단계를 따라

z_v

를 얻어낸다.

for k in range(K):

for v in V :

1-Hop 이웃 집합의 Embedding들을 하나의 Vector로 Aggregate한다. [hN(v)kh_{\mathcal{N}(v)}^khN(v)k​]

Node uuu의 Feature vector와 Aggregated Vector를 Concat한다

kkk에 대응되는 WK\bold{W}^KWK와 곱한뒤 Activation Function을 통과시킨다.

모든 Node에 대하여 연산이 끝나면 각 Vector를

L_2

Normalize한다.

z_v

h_v^K

Neighborhood Definition

실제로 학습시킬때는 Node의 이웃을 전부 사용하지는 않는다. 왜나하면, 모든 이웃을 정보로 사용할 경우 Memory 사용량과 계산의 양이 기하급수적으로 늘고, 예측하기 힘들기 때문이다. 따라서 사전에 고정된 크기의 이웃을 Uniform Sampling 해서 사용한다.

Learning the Parameter of GraphSAGE

GraphSAGE는 Unsupervised Setting으로 학습시키는 것이 기본적이며, Learning Objective는 가까이 있는 Node는 유사하게, 멀리 있는 Node는 극도로 다른 Embedding을 갖게 하는 것이다. 이를 위해 아래의 Loss Function을 사용한다. 구체적으로는 Random Walk 아래에서 같이 등장한 Node의 Embedding은 유사하게, Negative Sampling을 통해 추출된 Node의 Embedding은 다르게 임베딩 되도록 유도한다.

J_{\mathcal{G}}(\bold{z}_u) = -log(\sigma(z_u^Tz_v)) - Q \cdot \mathbb{E}_{{v_n}~P_n(v)} log(\sigma(-z_u^T z_{v_n})))

Notation

•

Node uuu : 관심있는 Node

•

Node vv v : Node uuu로 부터 시작한 고정 길이의 Random Walk 동안 등장한 Node

•

QQQ : Negatvie Sample의 갯수

•

PnP_nPn​ : Negative Sampling 분포

* 눈 여겨봐야 할 점은, 기존의 Transductive한 방법론 처럼 Look-Up Table 형태로 Embedding을 최적화한게 아니라, 이웃의 Feature로 부터 Embedding을 최적화 했다는점이다.

* 만약 Supervised Setting으로 학습시키고 싶을 경우, Loss Function을 Task Speicific한 것들로 바꾸어 학습시킬 수도 있다.

Aggregator Architectures

Graph는 다른 일반적인 Data와 달리 Order가 존재하지 않는다. 따라서 Aggeregator Function은 Permutation Invariant한 특징을 가져야한다. 동시에 표현능력도 있으면서 학습 및 미분이 가능해야 한다. GraphSAGE에선 이 조건을 만족하는 3가지 후보를 Aggregator로서 사용 및 검증 해 보았다.

Mean Aggregator

•

각 Vector의 원소값을 평균을 내 Aggregate하는 방법이다.

 LSTM Aggregator

•

Mean보다 표현능력이 뛰어난 방법이지만, 근본적으로 Permutation Variant하다. 

•

따라서 Input Node의 순서를 무작위로 섞어서 LSTM에 넣는다. 

•

(볼때마다 굳이? 하는 생각이 든다..)

Pooling Aggregator ()

•

Permutation Invariant하고 미분도 가능하다.

•

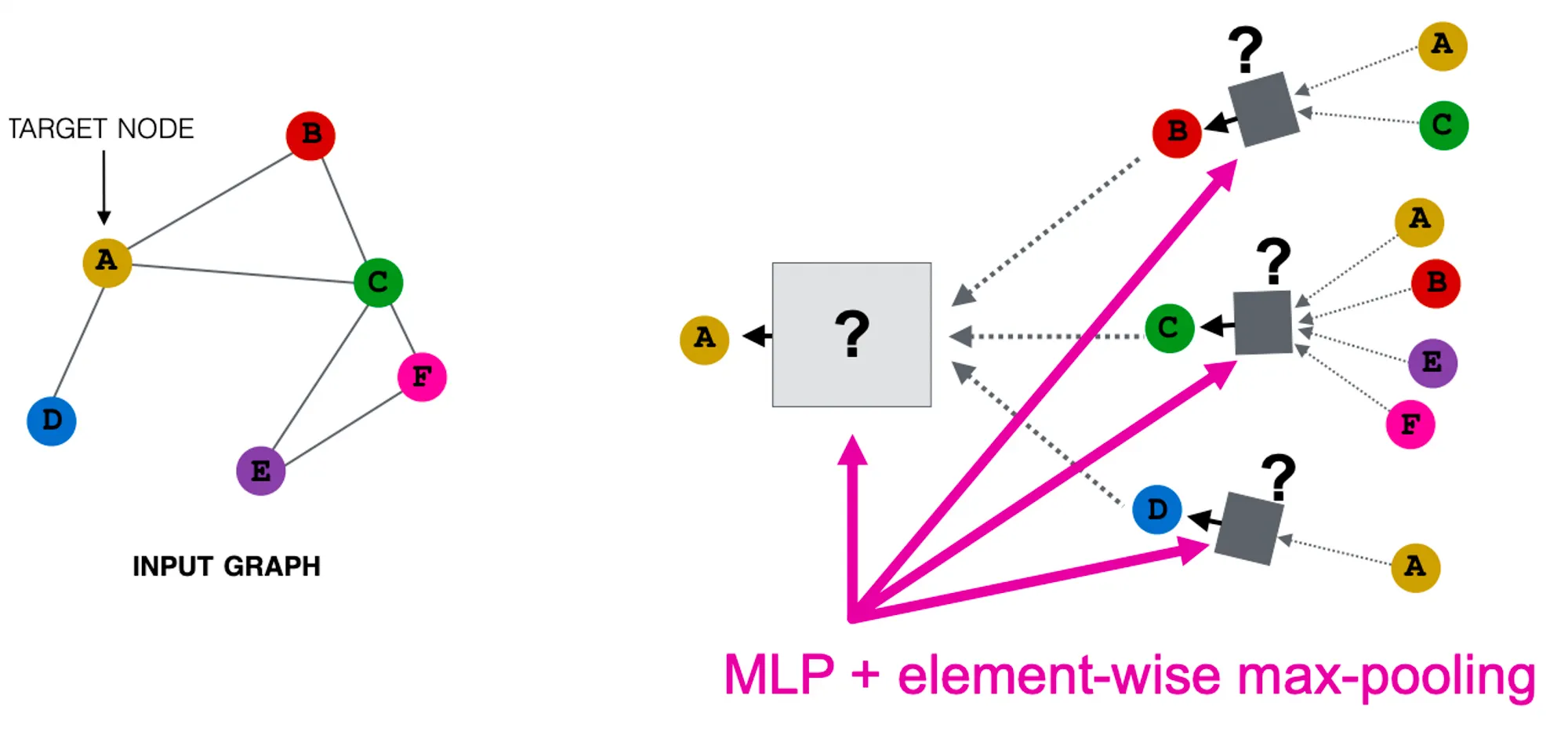
GraphSAGE에선 각각의 Embdding Vector를 FCN에 넣고 Element-Wise Max Pooling을 수행했다.

•

경험적인 실험 결과, FCN Layer는 1층만 쌓아도 잘 작동하고, Max나 Mean이나 성능에 큰 차이는 없었다.

AGGREGATE_k^{pool} = max( \{\sigma( W_{pool}h_{u_i}^k+b), \forall u_i \in \mathcal{N}(v) \})

Experiment

Dataset

Evolving Graph의 BenchMark로 2가지 Dataset을 사용했다. 첫 번째는 Web of Science Citiation Data를 이용해 논문 Classification을 수행했고, 두 번째는 Reddit Data를 이용해 Post가 속한 Community를 Classification했다.

Model SetUp

비교를 위한 Baselin으로는 4가지 모델을 사용했다.

Random Classifier 

Feature Based Logistic Regression 

DeepWalk 

Concat(Raw Feature, Deep Walk Embedding) 

Experiment Table

Insight 1 : Inductive Learning on Evolving Graph 

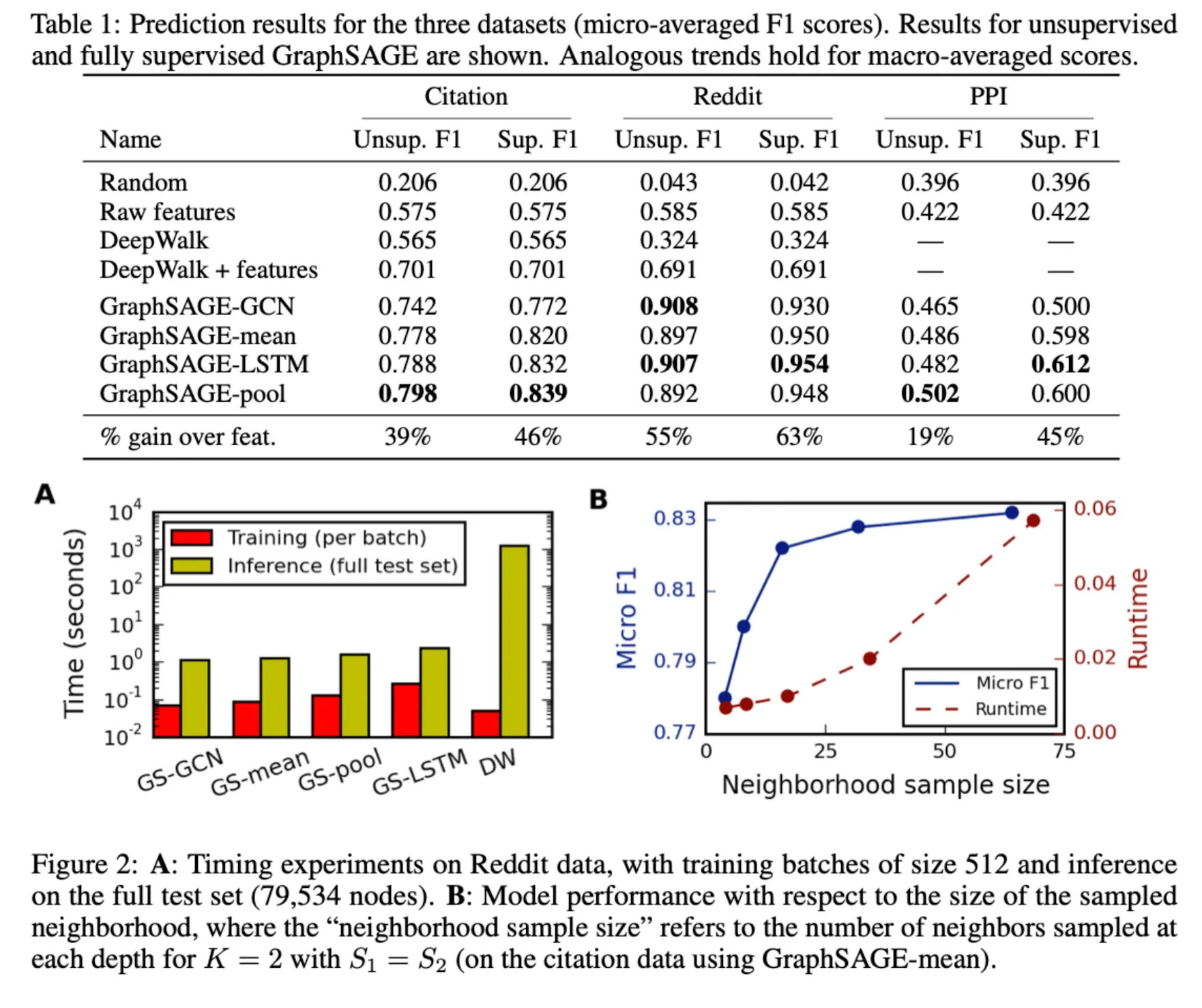
Evolving Graph인 Citation, Reddit Data에서 GraphSAGE가 Baseline을 압도하는 성능을 보였다. 재미있는 점은 LSTM을 Permutation Invaraint한 데이터에 사용했는데 좋은 성능을 보인다는 것이다. 또한 Unsupervised 모델들도 기존 Baseline을 압도하는 것으로 보아, GraphSAGE의 Framework 자체가 Graph Data에 대해 강력한 표현능력을 가지고 있음을 알 수 있다.

Insight 2 : Runtime and Parameter Sensitivity

Figure 2의 A를 보면 모델 별 학습및 추론에 걸리는 시간을 시각화 해놓았다. 학습에 걸리는 시간은 GraphSAGE와 DeepWalk간 큰 차이가 없지만, Unseen Node에 대한 Inference Timedms 100~500배 차이가 난다.

GraphSAGE Variant 실험에서는

K=2

일때가 Trade-off를 고려할 때 최적임을 찾아냈다. (이 부분은 BenchMark에 대한 최적값으로 보여 아마 Sparsity 기반으로 찾아나가야 할 듯)

Conclusion

GraphSAGE는 Unseen Node들에 대해 효과적인 Embedding을 하는 Novel 방법을 제시했다. 2017년 이후에도 GraphSAGE를 계승한 다양한 논문(GAT,PinSAGE, PinnerSAGE..)이 나와 지금까지도 영향을 미치고 있다.