Abstract
기존 Factorizing 방법은 Matrix를 Row, Column의 Latent Embedding으로 분해하고, 그 둘의 Product값이 Matrix의 값으로 나오도록 Embedding한다. 이런 식으로 특정 Data에 종속되어 있는 모델을 Transductive하다고 하는데, 학습할 때 Matrix에 등장하지 않았던 User, Item에 대한 예측이 어렵다.
이를 보완하기 위해 기존 연구는 추가적인 정보(Feature)를 사용하는데, 좋은 품질의 Feature를 사용할 수 있는 경우가 많지 않으며 Feature를 뽑는것도 또 하나의 Task다. Side Information이 없는 상황이라면 어떻게 Matrix 원소값을 예측 할 수 있을까?
Inductive Graph-based Matrix Completion(이하 IGMC)는 이런 문제를 해결하기 위해 나왔다. IGMC는 Graph에서 1-Hop Subgraph만을 추출해 GNN을 학습시킨다. 이런 방식으로 Transductive SOTA 모델에 근접한 성능을 보였으며, 학습할 때 등장하지 않았던 User,Item Pair에 대한 예측도 가능하다. 심지어는 Transfer Learning까지 가능함을 보였다. IGMC는 다음과 같은 3가지 사실을 보여주고 있다.
1.
Side Information 없이 Inductive한 모델을 만들 수 있으며, SOTA급 성능을 보인다.
2.
Node Pair를 둘러싼 Local Graph Pattern이 Link를 예측하는데 효과적이다.
3.
RecSys에선 Long-Range Depedency(큰 Hop)가 필수적이진 않다.
Introduction
Matrix Completion는 RecSys Task를 푸는 방법 중 하나이다. Matrix는 User와 Item를 각각 Row와 Column으로 두고 교차하는 지점에 관측된 Rating을 기입한 형태이며, Completion 한다는 것은 관측되지 않은 Interaction(교차하는 지점)의 값을 예측해 채워 넣는다는 뜻이다. 이렇게 예측된 Interaction을 추천에 사용한다.
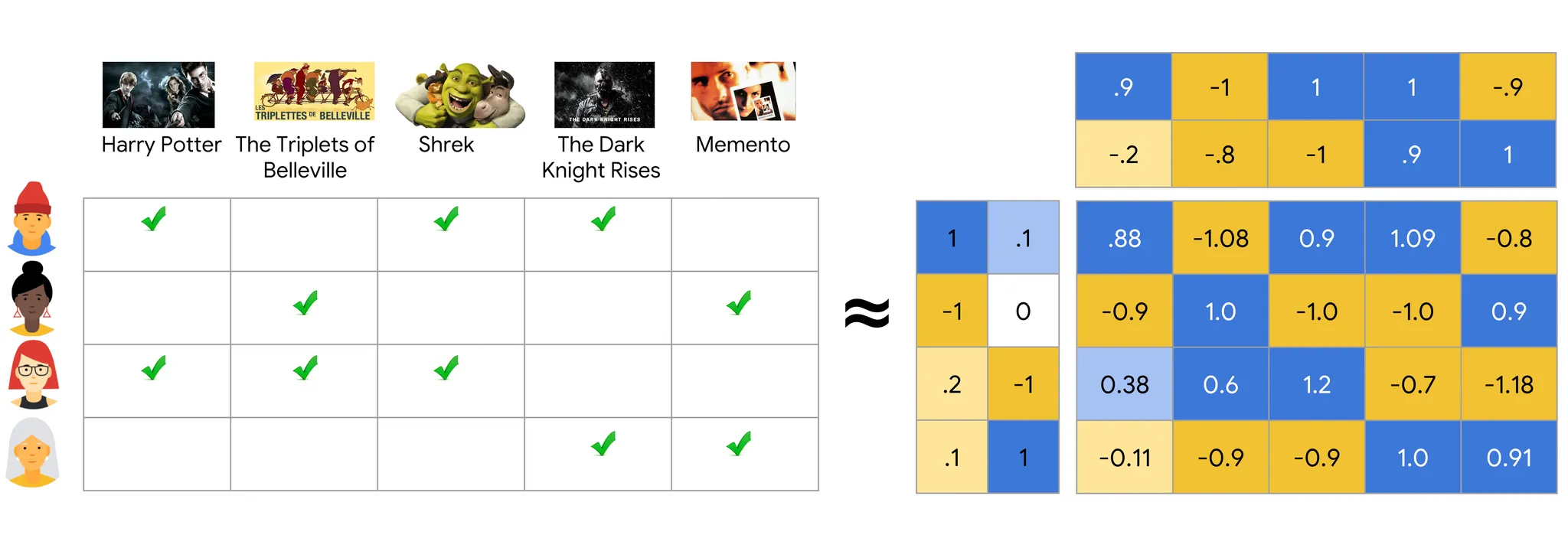
Matrix의 값을 채워넣는 방식 중 가장 기본적인건 Matrix Factorization 방식이다. Matrix Factorization은 Interaction을 User Latent Vector, Item Latent Vector의 내적이라고 가정하고 Latent Vector로의 Embedding을 모델링 하는 방식이다. Embedding을 구할 수 있는 Item과 User가 있다면 내적을 통해 Rating을 예측할 수 있다.
(User 와 Item 가 주어졌을때 User Latent Vector를 , Item Latent Vector를 라고 Notation)
그런데 Matrix Factorization은 태생적으로 Transductive하다. 다시 말해 학습중에 보지못한 User나 Item에 대해 일반화 하기 어렵다는 뜻이다. Rating Matrix의 Value가 수정되거나, 새로운 User나 Item이 추가되면 아예 새롭게 학습을 시켜야 한다는 큰 단점이있다.
이를 극복하고 Inductive한 Matrix Completion을 만들기 위해 Side Infomation을 사용하는 방법론이 제시되었지만(IMC), Side Information을 구할 수 없는 상황이나, Quality가 보장이 되지 않을 땐 부족한 성능을 보이는 한계가 있다.
(User Content Vector를 , Item Content Vector를 , Learnable Feature Weight를 로 Notation)
Side Information에 의존하지 않고 Matrix에 대해 Exchangeable한 Layer를 사용해 Inductive한 모델을 만든 연구도 있다. 그러나 Rating Matrix를 통째로 입력해 재구성된 Matrix를 만들어내는 형태라 수백만 User/Item이 있는 Case로는 확장이 불가능하다는 한계가 있다.
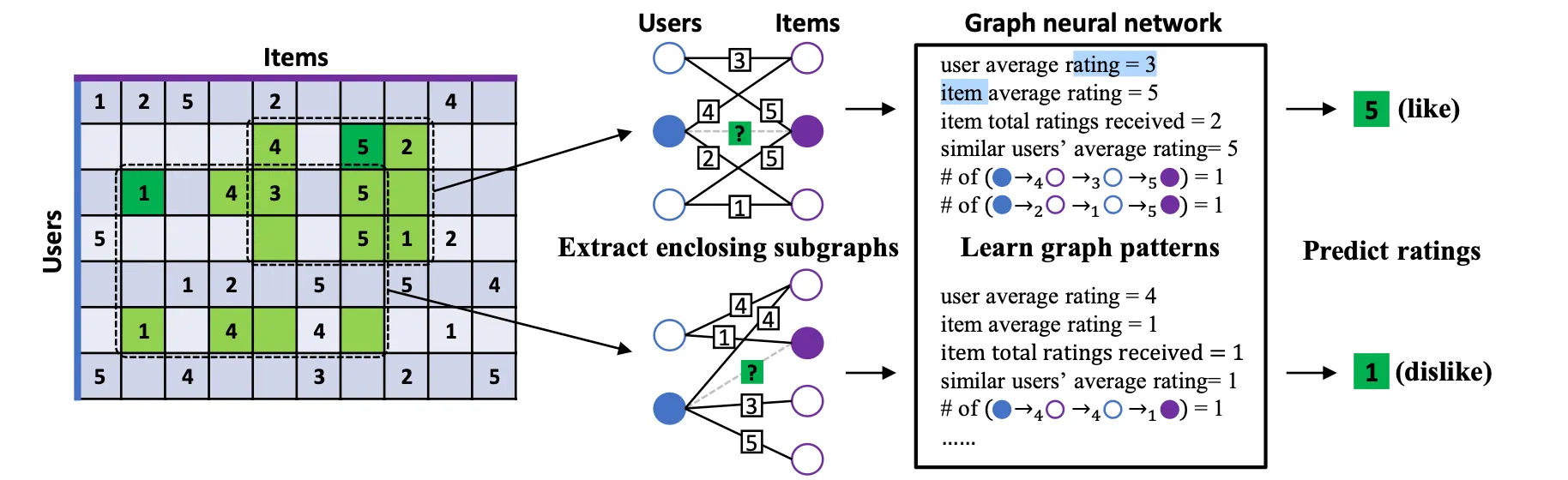
IGMC는 Rating Matrix를 이용해 Bipartite Graph를 만들고 Interaction을 Edge, Rating(점수)를 Edge의 Class로 사용한다. 즉 Matrix Completion를 Labeled Link Prediction 문제로 풀겠다는 의미이다. 이런 시도는 전에도 있었지만 IGMC가 Novelty를 갖는 부분은 Node Pair()의 Subgraph를 뽑아서 학습시킨다는 점이다. 이렇게 뽑힌 Subgraph는 GNN에 입력되어 구조적인 정보만으로 Link Class즉, Rating을 예측하도록 학습된다. 이 방법 덕분에 Side Information에 의존하지도 않고, Rating Matrix를 통째로 연산할 필요도 없는 효율적인 모델을 만들 수 있다.
IGMC
IGMC의 구조에 대해 설명하기 전에 Notation을 짚고 가자. 우선 Rating Matrix 에서 Bipartite Graph 를 얻어낸다. 는 User Node 와 Item Node 로 이루어져있는데 각각은 의 Row, Column과 같다. 사이의 Edge ()는 값을 가질 수 있는데, 이는 가 에게 준 Rating과 같다. 가능한 Rating의 집합을 로 표기하는데, MovieLens를 예로들면 1점부터 5점까지 Rating을 줄 수 있으므로
이다. 이웃의 집합은 와 같이 표현하는데, 이는 와 type으로 연결된 이웃 집합을 의미한다.
1. Enclosing SubGraph Extraction
IGMC의 첫 번째 파트는 SubGraph를 뽑는것이다. 가 주어지면 를 둘러싸고 있는 의 Subgraph를 뽑아서 GNN으로 Rating을 Regression한다. SubGraph를 추출하는 과정은 다음과 같다.
BFS로 각 Hop마다 직전 Hop에서 구해진 Node들의 이웃을 가져오는 방식으로 SubGraph를 만든다. 번 반복이 끝났으면 간 Edge를 제거하고 학습을 통해 예측하도록 한다.
2. Node Labeling
IGMC의 두 번째 파트는 SubGraph의 각 Node에 Integer Label(일종의 ID)를 달아주는 것이다. 다른 역할을 하는 Node은 다른 Label을 갖도록 하는것이 목적인데, 이상적인 시나리오는 (1) Target Node와 Context Node를 구분하고 (2) Item Node와 User Node를 구분할 수 있도록 만드는 것이다. 이 시나리오를 만족시키기 위해서 다음과 같이 Node Labeling을 진행한다.
1.
Target User와 Target Item에 각각 0, 1을 할당한다.
2.
번째 Hop에서 구해진 User에 대해선 를 할당하고 Item에 대해선 을 할당한다.
이 과정을 거치고 나면 위의 시나리오를 만족하면서, Target Node와의 거리(Hop)도 표현해 줄 수 있다. 다양한 대안이 있지만, 이 방법도 충분할 정도로 잘 작동하는 것을 경험적으로 확인했다. Global Graph의 어떤 정보도 사용하지 않기때문에, Global Graph가 아예 바뀌어 버려도 유사한 Local 이웃구조를 가진 SubGraph에 대해 예측을 잘 할 수 있다. 이렇게 할당된 Node Label은 Initial Node Feature로 활용된다.
3. GNN Architecture
IGMC의 세 번째 파트는 SubGraph로부터 Rating을 예측하도록 GNN을 학습시키는 것이다. 기존 연구(GCMC)는 (1) 전체 Graph에 (2) Node-Level GNN을 적용해 (3) Node Embedding을 추출하고 그 값을 Decoder에 넣어 Rating을 예측했다. IGMC는 이와 다르게 (1) 관심있는 노드의 인접 SubGraph에 (2) Graph-Level GNN을 적용해 (3) 직접 Rating을 예측한다.
IGMC의 GNN은 SubGraph의 인접 Node로 부터 Feature를 뽑아내는 Message Passing Layer와 그 Feature를 Graph-Level로 Summarize하는 Pooling Layer로 구성되어 있다.
Message Passing Layer는 GCN을 이용하는데, 풍부한 표현 능력을 위하여 Edge Type(Rating)에 따라 다른 가중치를 사용하는 R-GCN을 이용한다. 수식으로 표현하면 다음과 같다.
은 Layer 에서 Node 의 Feature 벡터를 의미한다. 는 Weight Matrix를 의미하며 Edge Type 에 따라 다른 를 갖게 된다. Message Passing Layer를 여러개 쌓을 수도 있는데, 이때엔 Layer마다 Activation을 적용해 준다. Message Passing이 끝나면 각 layer에서 추출된 Feature를 합쳐 Final Representation 로 사용한다.
Pooling Layer는 Sum, Average등 다양한 선택지가 있는데 경험적으로 실험해본 결과, IGMC는 Concat을 이용한다. 또 Pooling에는 Target Item, Target User Node만 이용한다. 이를 수식으로 표현하면 다음과 같다.
이렇게 Grah-Level Representation 가 구해지면, 2-Layer MLP를 이용해 Rating()을 예측한다. 이때 Activation Function은 를 이용한다.
4. Model Training
Loss Function은 일반적인 MSE을 사용하고, 거기에 Adjacent rating regularization(이하 ARR)을 더해 사용한다. 이때 ARR은 각 Relation Type간의 거리를 나타내기 위한 Term이다.
ARR을 설명하기 위해 영화에 Rating을 주는 상황을 예로 들면, 4~5점은 영화가 좋다고 평가한 경우이고 1점은 영화가 안좋다고 평가한 경우일 것이다. 4점은 5점과 유사한 평가고 1점과 크게 다른 평가라고 볼 수 있는데, R-GCN은 각각의 Rating을 독립적으로 다루므로, 이러한 정보를 명시적으로 모델링 할 수 없다. 이를 보완하기 위해 가까운 Rating 끼리 유사한 Weight를 갖게 하도록 하는 Technique이 ARR이다. 수식으로 표현하면 다음과 같다.
Graph-Level GNN vs. Node-Level GNN
이전 Graph Matrix Completion 방법론들(GCMC, PinSage)은 Node-Level GNN을 이용하는데, 근본적으로 관심있는 Node 쌍(Item, User)의 Subtree를 독립적으로 Encoding하게 된다. 이 경우 두 Subtree간의 Interaction을 모델링 할 수 없다.
위의 그림은 (a) Graph-Level GNN의 Subtree와 (b) Node-Level GNN의 Subtree를 시각화 한 것이다. Node-Level GNN은 (b) 두 Node가 고립되어있든, (a) Subtree안에서 풍부한 연결을 가지고 있든 똑같은 연산으로 처리해버린다.
Graph-Level GNN은 Sub-Graph에 대해서만 학습을 하므로, GCN Layer를 충분히 쌓으면 두 케이스를 구별 할 수 있으며, 쌓을수록 표현능력이 강력해져 WL-Kernel 수준 까지 도달하는 것이 증명되었다. 그러나 Node-Level GNN은 Sub-Graph Boundary가 없으므로, 관계없는 Node에 대해 Convolution을 수행하고 Over Smoothing을 일으킨다.
Graph-Level GNN도 단점은 있는데, Target Node 쌍이 주어질 때 마다 Sub-Graph에 대해 연산을 수행해야 하므로 Node-Level GNN에 비해 연산비용이 비싸다. 따라서 IGMC를 실제로 사용하려면 Sub-Graph Edge의 최대갯수 를 적절히 제한해 연산 비용을 줄여야한다.
Experiments
Matrix Completion Task에 사용되는 Dataset 5개(Flixster, Douban, YahooMusic, ML-100K, ML-1M)에 대해 실험을 수행했다. IGMC는 pytorch_geometric 을 이용해 구현했으며, 사용한 모델은 4-Layer
R-GCN 이다. GCN의 Hidden Dimension은 32를 사용했고, 예측을 위한 MLP Layer는 128 dims에 0.5 Dropout를 적용했다. SubGraph는 1-Hop에 대해서만 추출했으며, 이 정도로 충분함을 확인했다. (Hop을 늘려도 Training Time 대비 적은 성능 향상을 보였다.) 는 0.001으로 두었다. 학습할 때는 Batch Size 50, Learning Rate 0.001을 사용했으며 20 Epoch마다 Learning Rate를 0.1배로 만들었다.
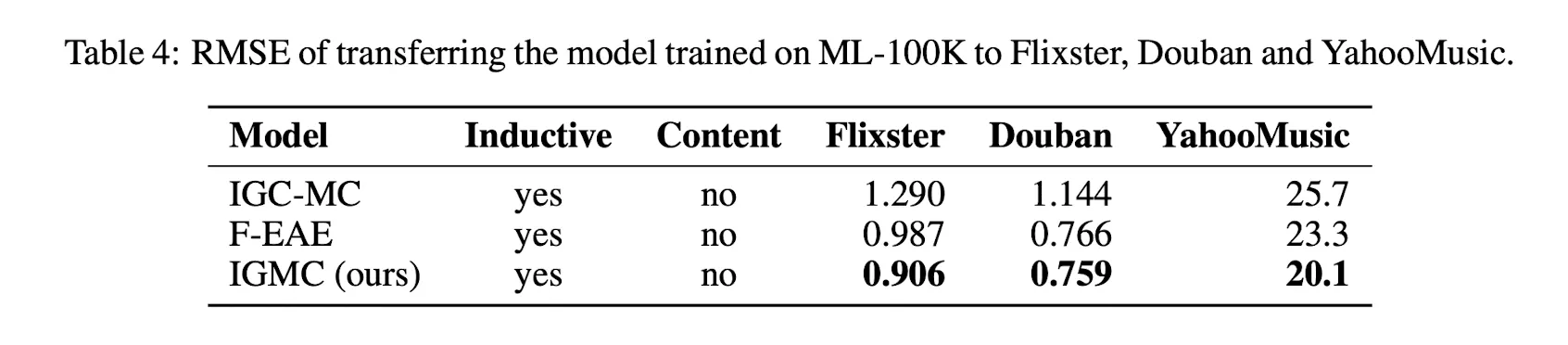
그 결과 Side Information없이도 기존 GNN 대비 우수한 성능을 보였으며, Sparse한 Graph에 대해서도 Transductive한 모델보다 우수한 성능을 보이고, Transfer Learning까지 가능한 모습을 보였다.