Abstract
GCN in Collaborative Filtering(이하 CF)
•
GCN은 추천, CF Task에서 강력함
•
그러나 “왜” 강력한지는 명확히 규명 안됨
•
GCN의 용도를 생각해보면 Node, Graph Classification Task를 위해 만들어진 프레임워크임
•
따라서 최적화된 구조는 아닐 수 있음
•
실증적으로 실험해 봤더니 FeatureTransform과 Actionvation Function이 성능에 끼치는 영향이 미비함
•
오히려 학습이 잘 안되고 추천 성능이 떨어질 때도 있음
LightGCN
•
저자들은 GCN의 핵심 기능인 Neighborhood Aggergation만 남김
•
Linear한 변환만 거쳐서 학습시키고, 모든 레이어의 가중합을 임베딩으로 사용함
•
간결하고 직관적인 구조임에도, SOTA보다 뛰어난 성능을 보임
Conclusion
•
CF Task GCN의 불필요하게 복잡한 부분을 걷어낸 LightGCN을 제안함
•
LightGCN은 Light Graph Conv와 Layer Combination으로 이루어져 있음
•
LightGraph Conv는 Feature Transform, Activation을 걷어내서 학습 난이도가 쉬움
•
Layer Combination은 모든 레이어의 임베딩 가중 합을 이용해 최종 임베딩을 얻어냄
•
일종의 Residual과 같은 효과를 가지며 Over Smooth를 어느정도 방지함
•
위와 같은 특징을 가진 LightGCN이 SOTA모델보다 가볍고 강력한 CF 모델임을 실험을 통해 증명함
Figures
Summary
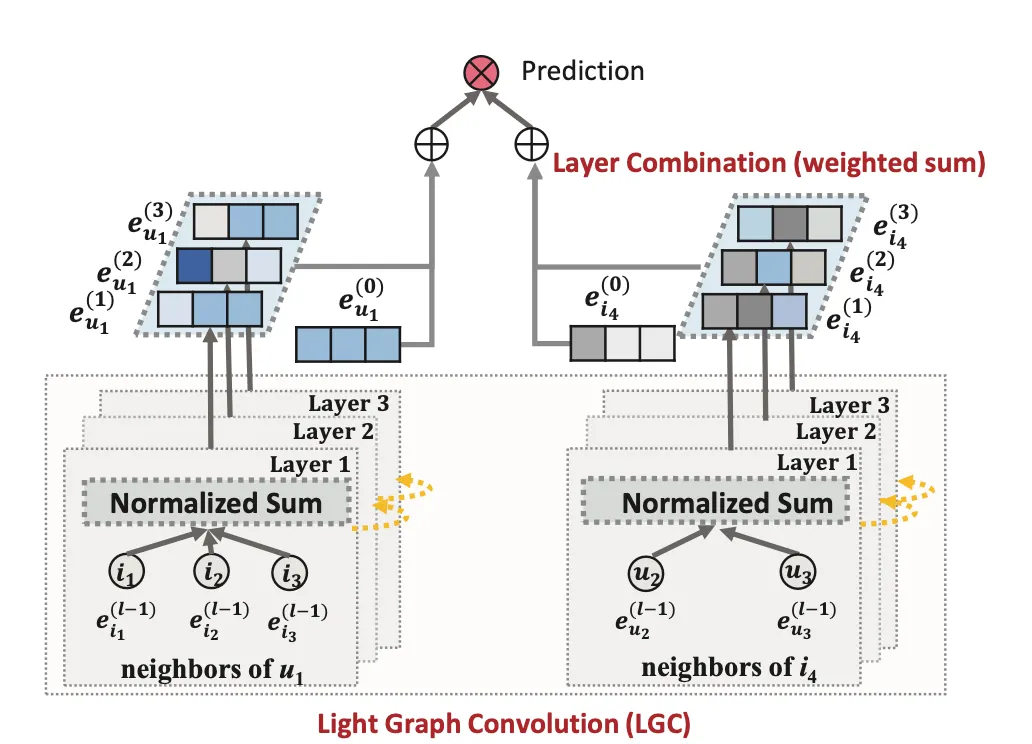
LightGCN은 User-Item Bipartite Graph를 Transductive하게 모델링 하는 Task에 대해 다룬다.
Light Graph Convolution
•
각 LGC Layer는 이웃 Embedding을 전부 더하고 이웃 수에 따라 Normalize한다.
•
자신의 Embedding은 고려하지 않는다.
•
학습되는 파라미터는 없다.
Layer Combination
•
개의 LGC Layer 연산이 끝나면, 각 Layer에서의 결과값을 가중합해 최종 Embedding으로 사용한다.
•
이때 가중치는 파라미터로 학습시킬 수도 있고, 직접 지정해줄 수도 있다.
•
직접 설정해줄 경우 일 때 일반적으로 성능이 좋았다.
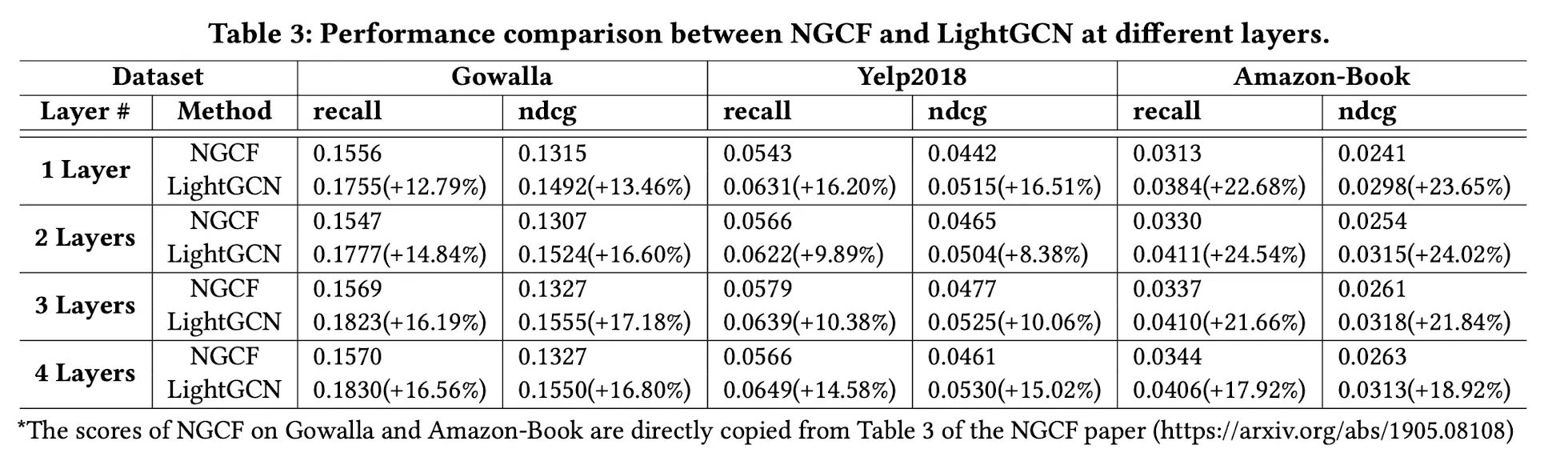
Experiment
NGCF : 당시 SOTA