Home
///
///
🙃

리뷰 : HybrIK

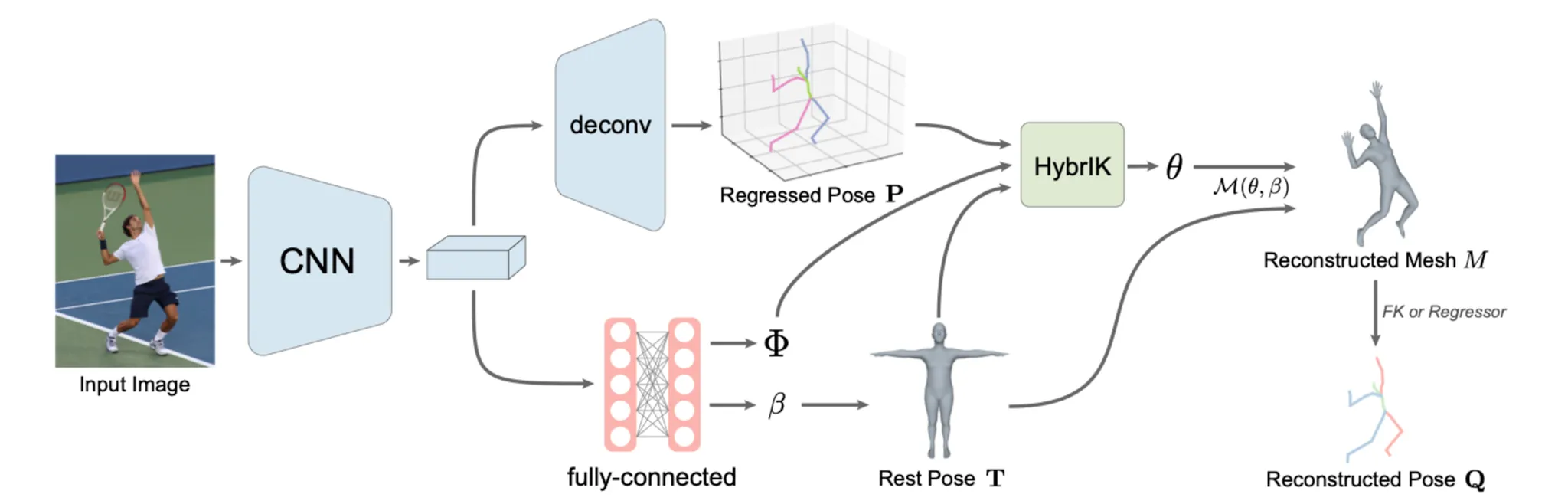
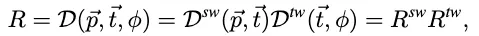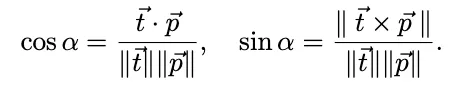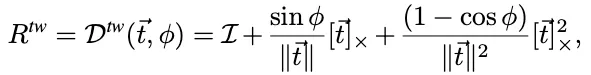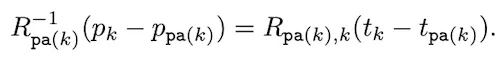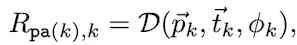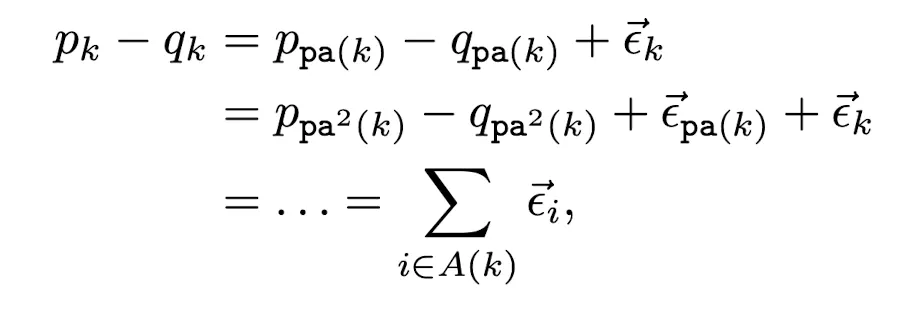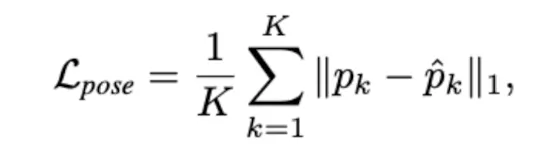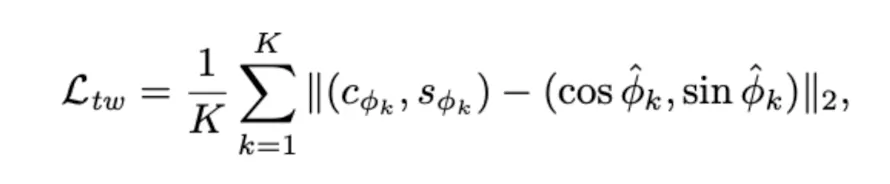A Hybrid Analytical-Neural Inverse Kinematics Solution for 3D Human Pose and Shape Estimation 리뷰

0. Abstract

Model Method
•
SMPL과 같은 Model을 기반으로 하는 Estimation은 Pose(θ\theta), Shape(β\beta) Parameter 들을 예측해 3D Mesh를 만든다.
•
그러나 Parameter는 극도로 Non-Linear하고, Image-Model Misalignment 문제가 존재해 아쉬운 성능을 보인다.
Volumetric Method
•
CNN과 Volumetric Representation을 이용한 3D Key Points Estimation은
•
Pixel-level에서의 Localization이 가능한 정도의 성능을 달성하였으나
•
비현실적인 신체 구조로 Key Points를 예측하는 경우가 잦다. (Constraint이 없다)
Hybrid Method(HybrIK)
•
상술한 두 Method의 장점은 살리고, 단점을 보완하기 위한 hybrid inverse kinematics solution (HybrIK)을 제시한다.
•
HybrIK은 비교적 정확한 3D Joints를 Relative Rotation으로 변환해 3D Mesh를 만든다.
•
이 방법을 통해 SOTA를 달성했다.

1. Introduction

이전 방법론들은 어땠는가?
Optimization-Based Approach (Model)
•
Iterative Fitting을 통해 Pose(θ\theta), Shape(β\beta) 예측
•
Statistical Model을 2D Projection을 통해 Error를 줄이도록 Tune됨
1.
(한계) Optimization Problem은 Non-convex하며, 시간이 오래 걸림
2.
(한계) 결과가 Initialization에 대해 민감하게 반응함
Learning Based Approach (Model)
•
Optimization 방법론의 한계때문에 주목받기 시작
•
NeuralNet을 이용해 Model의 Parameter를 직접적으로 구함(Regress)
1.
(한계) Parameter Space가 매우 Abstract함
2.
(한계) Mapping Function을 학습시키기 어려움
3D Keypoint Estimation
•
Volumetric Heatmap을 이용해, 3D Joint Location을 학습시켜 인상적인 성능을 달성함
•
(한계) Body Bone Length와 같은 Prior가 없어, 좌우 비대칭 등의 Unrealistic Body Structure를 보일 수 있음
•
우리는 비교적 좋은 성능을 활용하기 위해 3D Joint와 Body Mesh를 Collaboration할 예정
1.
3D Keypoints 를 이용해 3D Body Mesh를 Estimation 개선
2.
Shape(β\beta) Prior를 이용해 3D Keypoint Estimation의 Unrealistic Body Structure 문제를 해결
저자가 제시하는 HybrIK이란 무엇인가?
IK : Inverse Kinematics
•
특정 Joint의 Position이 주어졌을 때, 이를 만들어 내는 Rotation을 찾아내는 수학적 방법
•
Unique한 정답이 없기에, ill-Posed Problem이다.
Rotation Decomposition
•
HybrIK에선 Relative Rotation을 Twist, Swing 으로 분해해서 모델링한다.
•
Twist는 NeuralNet을 이용해 예측하고, Swing은 Analytical 하게 추론한다.
HybrIK
1.
3D Keypoints Estimation을 IK하여 Decomposed Relative Rotation을 구하고 (IK)
2.
이를 Pose(θ\theta)로 활용해 3D Mesh를 만들어 낸다. (Hybrid)
3.
Profit ( SOTA 달성 )

2. Realated Work

3D Keypoint Estimation
•
분류 :
◦
Single-Stage : Image로부터 3D Joint Location을 바로 예측하는 방법
◦
Two-Stage : 2D Pose를 예측한 뒤 Regression, Dictionary등을 이용해 3D로 Lift하는 방식
•
장점 : Powerful Backbone + 2D Heatmap + Lift 구조를 이용해 인상적인 성능 도달 가능
•
단점 : 인체 구조에 대한 정보가 명시적으로 주어지지 않으므로, 비현실적인 3D Skeleton을 예측할 수 있다.
•
결론 : HybrIK는 3D Keypoint와 Parametric 모델을 같이 사용함으로서, 단점을 극복하고 장점을 살렸다.
Model-based 3D Pose and Shape Estimation
•
장점 : DownStream Task에 활용 가능한 Controllable Body Mesh를 예측한다.
•
단점 : RGB Image → Rotation(θ\theta), Shape(β\beta) Mapping을 학습시키기 어렵다.
•
결론 : HybrIK은 Pixel-Aligned 3D Joints를 Rotation 예측에 활용함으로서, 단점을 극복하고 장점을 살렸다.
Body-part Rotation in Pose Estimation
•
발전 : Angle 예측 → FK Layer 활용 → Quaternion, Rotation Matrices, Euler Angle활용 등등..
•
한계 : 학습시키기 어렵고, 추가적인 Fitting procedure가 필요하다
•
결론 : HybrIK은 3D Joint를 직접적이고 정확하게 FeedForward시켜 Rotation을 구한다.
Inverse Kinematics Process(IK)
•
분류 :
◦
Numerical : IK를 구현하기 쉽지만, Iterative Optimization에 시간이 너무 많이 드는 방법
◦
Heuristic : IK를 구현하기 위한 효율적인 방법
◦
NeuralNet : 최근 IK를 구현하기 위한 방법으로 주목받고 있음
•
결론 : HybrIK은 Twist-Swing Decomposition을 통해 Analytical의 직관성과 NeuralNet의 유연성을 혼합함

3. Method

3-1 Preliminary

QQ : Reconsturcted Pose {qk}k=1K\{q_k\}_{k=1}^K TT : Rest Pose Templete {tk}k=1K\{t_k\}_{k=1}^K RR : Relative Rotations {Rpa(k),k}k=1K\{R_{pa(k),k}\}_{k=1}^K
KK 가 Body Joint의 갯수로 정의될 때
•
qk∈R3q_k \in \mathbb{R^3} 는 kk 번째 Joint의 Recontructed 3D Location을 의미한다.
•
tk∈R3t_k \in \mathbb{R^3} 는 kk 번째 Joint의 Rest Pose Templete Location을 의미한다.
•
pa(k)pa(k)는 kk 번째 Joint의 부모 Joint의 Index를 반환하는 함수이다.
•
Rpa(k),kR_{pa(k),k} 는 kk 번째 Joint의 부모 Joint에 의존한 Relative Rotation을 의미한다

Forward Kinematics(FK)

Q=FK(R,T)Q = FK(R,T) : Rest Pose Templete을 회전시켜 Reconsturted Pose를 얻어낸다.
qk=Rk(tk−tpa(k))+qpa(k)q_k = R_k(t_k − t_{pa(k)}) + q_{pa(k)}
•
FK는 Root Joint부터 Leaf Joint에 해당하는 Body Part를 Reculsive하게 회전시키면서 수행된다
1.
Templete을 이용해 Bone Length를 구하고 (tk−tpa(k))(t_k − t_{pa(k)})
2.
Rotation을 시켜준뒤 Parentes의 Position을 더한다.
3.
Reconstructed Position 완성 ^-^

Inverse Kinematics(IK)

R=IK(P,T)R = IK(P,T) : Input Body Joints (P={pk}k=1KP =\{p_k\}_{k=1}^K) 를 만들 수 있는 Relative Rotation을 얻어낸다. |
pk−ppa(k)=Rk(tk−tpa(k)) p_k −p_{pa(k)} =R_k(t_k −t_{pa(k)}) (P는 Input Pose Position)
•
IK는 FK의 Reverse Process 이며, 잘 수행된다면 FK의 등식을 만족한다.
•
FK는 Well-Posed(조건이 잘 정의되어있음?) 문제지만
•
IK는 Target Joint를 만족시키는 Solution이 없거나, 여러 개 일수 있어 ill-Posed 문제로 여겨진다

3-2 Hybrid Analytical-Neural Inverse Kinematics

•
Direct Regression을 이용해 Relative Rotation을 구해 Human Body Mesh를 추정하는 것은 매우 어려운 일이다.
•
HybrIK은 3D KeyPosition을 이용해 3D Body Mesh Estimation을 Boost 한다
•
3D Joint는 Relative Rotation을 Unique하게 결정하지 못하므로 Rotation을 Twist, Swing 2가지로 나눈다.
◦
Twist : Visual Cues(Image Feature)를 이용해 NeuralNet 으로 추론됨
◦
Swing : 3D Joint를 이용해 Analytically 추론됨

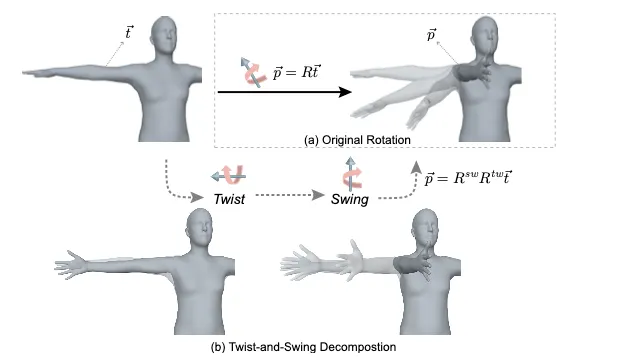
Twist-and-Swing Decomposition

•
HybrIK에선, 각 Body Joint는 3 DoFs(자유도)로 가정됨
•
우측 그림에서 볼 수 있듯이 Rotation은 Twist (RtwR^{tw}), Swing(RswR^{sw})으로 나눠질 수 있음
•
(Pose Templete Body-Part Vector) t⃗\vec{t} 와 (Target Vector) p⃗\vec{p} 가 주어졌을 때 RR의 수식은 다음과 같다
◦
ϕ\phi 는 NeuralNet으로 예측된 Twist Angle 을 의미한다.
◦
Dsw(⋅)D^{sw}(\cdot)은 Swing Rotation을 추론하는 Closed Form Solution을 의미한다.
◦
Dtw(⋅)D^{tw}(\cdot)는 ϕ\phi 를 Twist Rotation으로 변환한 것이다.
◦
이때, RR은 p⃗=Rt⃗\vec{p} = R\vec{t} 를 만족해야 한다.
Swing
•
t⃗\vec{t} , p⃗\vec{p} 와 수직한 Axis인 n⃗\vec{n} 을 가진다 (n⃗=t⃗×p⃗∥t⃗×p⃗∥\vec{n} = {\vec{t} \times\vec{p} \over \|\vec{t} \times\vec{p}\|})
•
angle α\alpha는 다음을 만족한다.
•
위 조건 아래서, Rodrigues Fomula을 이용해 RswR^{sw}의 Closed-Form 수식을 얻을 수 있다.
Rsw=Dsw(p⃗,t⃗)=I+sinα[n⃗]×+(1−cosα)[n⃗]×2R_{sw} = D^{sw}(\vec{p},\vec{t}) = I + sin α[\vec{n}]× + (1 − cosα)[\vec{n}]^2_×
[n⃗]×[\vec{n}]_×는 n⃗\vec{n} 의 Skew Symmetric Matirx, II 는 3×33 \times 3 Identity Matrix
Twist
•
t⃗\vec{t} 자신을 기준으로 ϕ\phi 만큼 회전하는 Rotating
[t⃗]×[\vec{t}]_×는 t⃗\vec{t} 의 Skew Symmetric Matirx

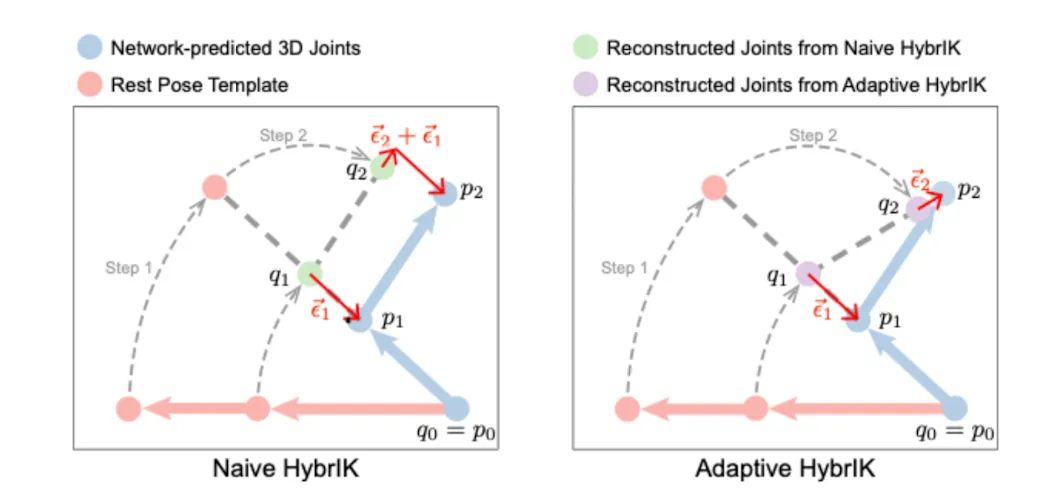
Naive HybrIK & Adaptive HybrIK

Naive HybrIK
•
Global Rotation인 RkR_k 대신, Relative Rotation Rpa(k),kR_{pa(k),k}를 사용해 문제를 푼다.
◦
Global Rotation에 대해 바로 Decompose할 경우 부모들의 Rotation에 의존하게 되고 변동이 커져 학습이 어려워진다.
1.
R0R_0인 Global Rotation을 Spine, Left Hip, Right Hip Position을 SVD해서 구한다.
2.
Rpa(k)R_{pa(k)}를 알고있다고 가정하면 다음 식을 구할 수 있다.
•
이때 pk⃗=Rpa(k)−1(pk−ppa(k))\vec{p_k} = R_{pa(k)}^{-1}(p_k −p_{pa(k)}) , tk⃗=(tk−tpa(k))\vec{t_k} = (t_k - t_{pa(k)}) 라고 두면 Relative Rotation을 구할 수 있다.
Rotation Matrices는 Orthogonal하므로, Transpose와 Inverse가 같다 → 미분 가능하다
3.
kk에 대해 반복한다.
ϵ⃗\vec\epsilonin Naive HybrIK
•
Naive HybrIK은 다음과 같은 가정을 따른다 : ∣∣pk−ppa(k)∣∣=∣∣tk−tpa(k)∣∣||p_k - p_{pa(k)}|| = ||t_k - t_{pa(k)}||
•
tt와 달리, Estimation을 통해 얻어진 pp는 Structure가 일정하지 않다.
•
이때, 발생한 Error를 ϵ⃗\vec\epsilon 으로 정의하면 다음과 같은 식이 성립한다.
◦
pk−ppa(k)=Rk(tk−tpa(k))+ϵ⃗kp_k - p_{pa(k)} = R_k(t_k - t_{pa(k)}) + \vec\epsilon_k
▪
(ϵ⃗\vec\epsilon 는 pk−ppa(k)p_k - p_{pa(k)}와 방향이 같으며)
▪
(∣∣ϵ⃗∣∣=∣∣pk−ppa(k)∣∣−∣∣tk−tpa(k)∣∣||\vec\epsilon|| =||p_k - p_{pa(k)}|| -||t_k - t_{pa(k)}|| 이다)
•
FK 공식과, 위의 식을 이용하면 다음과 같은 식을 얻을 수 있다.
Naive 식
•
식을 보면 알 수 있듯이, Error가 사라지지않고 누적되는 형식인데, 말단으로 향할수록 불안정성이 더 커진다.
Adaptive HybrIK
•
Adaptive HybrIK은 Error 누적 문제를 해결하기 위해 고안되었다.
•
Adaptive HybriK은 Reconstruct가 일어날 때 마다 Target Vector를 Adaptive하게 수정하는 방식이다.
•
이렇게 하면 Naive식이 다음과 같이 변한다
◦
pk−qpa(k)=Rk(tk−tpa(k))+ϵ⃗kp_k - q_{pa(k)} = R_k(t_k-t_{pa(k)}) + \vec\epsilon_k
◦
pk−qk=ϵ⃗kp_k - q_k = \vec\epsilon_k
•
Naive와 달리 ϵ⃗\vec\epsilon 이 Tree를 따라 누적되지 않고, 그 때의 Joint에만 의존한다.
•
대신 Adaptive는 Rotation을, 항상 ϵ⃗\vec\epsilon 를 줄이는 방향, 즉 Target Joint 방향으로 구할 것이다.

3-3 Learning Framework

Architecture

3D Keypoint Estimation
Backbone : ResNet Heatmaps : Deconv + Soft-Argmax Loss : L1 Distance
•
간단하고 효과적인 Backbone ResNet 사용
•
Output Feature에 Deconv → 1x1 Conv → Soft-Argmax를 통해 3D Joint Position 획득
•
Loss는 L1 Loss를 평균 낸 값을 이용
Twist Angle Estimation
Twist : ϕ\phi 를 바로 사용하는 대신, 불연속성을 피하기 위해 2차원 벡터 (cϕk,sϕkc_{\phi_k}, s_{\phi_k})로 분할한다.
•
Ground-Truth Twist를 (cϕk,sϕkc_{\phi_k}, s_{\phi_k}) 를 분할 후 ,예측값과 비교
•
L2 Loss 사용
Collaboration with SMPL
Shape (β\beta) : 기본 Shape에 β\beta 에 따른 Offset을 적용함으로서 Rest Pose TT 획득 : Lshape\mathcal{L}_{shape} Pose (θ\theta) : HybrIK으로 얻어진 θ^\hat\theta 와 비교함 Lrot\mathcal{L}_{rot} Loss : L2 Distance
Implementation Details
•
ResNet : ImageNet Pre-Train, ResNet-34 사용
◦
ResNet Output이 2 Branch로 나눠짐
▪
Fully Connected Branch
•
Avg Pooling → 1024 FC → Dropout → 1024 FC → Dropout → 56 FC
•
56 FC : (10 for β\beta , 23 * 2 for Φ\Phi)
▪
3D Heatmap Branch
•
Deconv와 1x1 Conv를 거쳐 PP 생성
•
Training
◦
Epoch : 140
◦
Optimizer : Adam
◦
Learning Rate : 0.001으로 시작해, 90~120 Step에서 Factor 10으로 Reduce
◦
Batch Size : 8 GPU를 사용했으며 32 per GPU : 32 * 8
◦
Loss :
L=Lpose+μ1Lshape+μ2Lrot+μ3Ltw\mathcal{L} = \mathcal{L}_{pose} +\mu_1\mathcal{L}_{shape} +\mu_2\mathcal{L}_{rot} +\mu_3\mathcal{L}_{tw} (μ1=1,μ2=μ3=0.01\mu_1=1,\mu_2=\mu_3=0.01 )

4. Empirical Evalution

4.1 Dataset

•
Train : 3DHP(Train Set), H3.6M(S1, S5, S6, S7, S8), MSCOCO(Train Set)
•
Test : 3DPW, 3DHP(Test Set), H36M(Test Set),

4.2 Ablation Study

Rotation Decomposition과 HybrIK Algorithm이 실제로 효과가 있는가 ?
Analysis of the Twist Rotation
•
Twist Decompostion 관련 실험
•
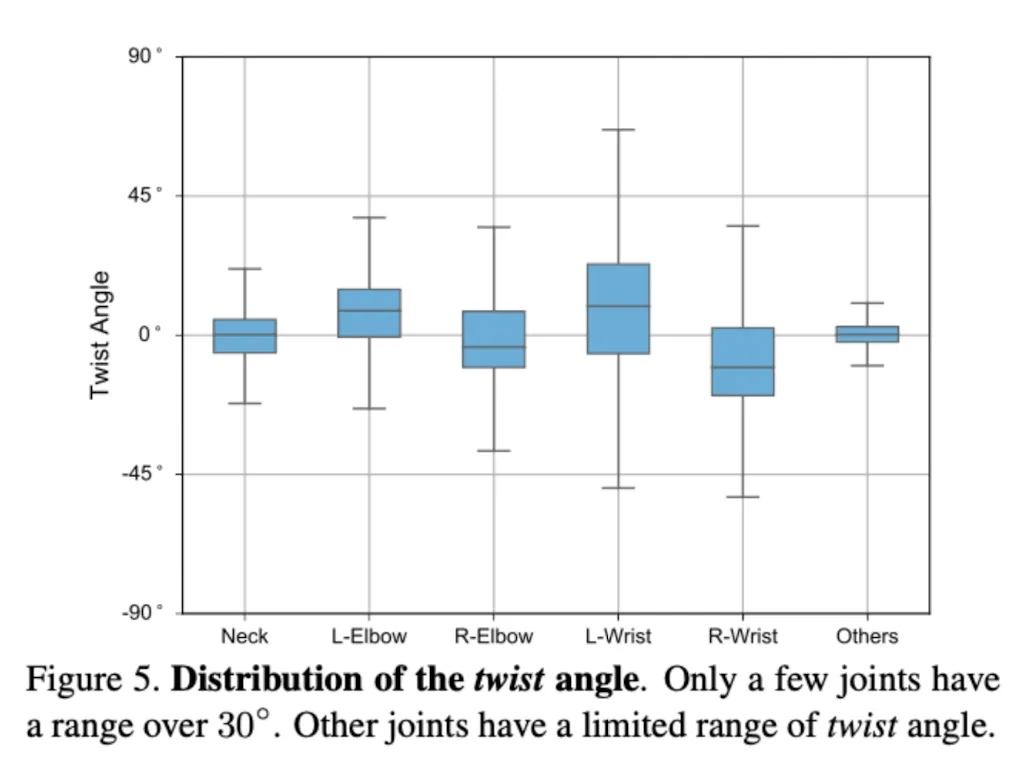
우측 그림은 3DPW의 Twist Distribution이다.
•
물리적 제한 때문에, Neck, Elbow, Wrist 을 제외하곤 30도 이내임을 볼 수 있다.
•
추가적으로 Twist가 Pose와 Shape에 끼치는 영향을 확인하는 실험을 해봤다.
◦
Ground Truth Parameter를 가져와 Twist를 교체해 보면서 Reconstruct Error를 재봄
1.
[-π\pi,π\pi] 사이의 Random Value
2.
Estimated Value
3.
0으로 고정
•
Twist가 정확할수록 GT와 비교해 Angle, Vercites 결과물 차이가 줄어듦
Robustness of HybrIK
•
Adaptive가 Naive에 비해 우수함을 입증하기 위해 비교 실험
1.
G.T Paramter가 주어졌을 때, Extra Error 비교
→ 무시할 만한 정도의 Error 발생
2.
G.T Paramter Input에 Noise를 넣어 Robustness 비교
→ Noisy한 Input에 대해서는 Adaptive가 나은 결과를 보임
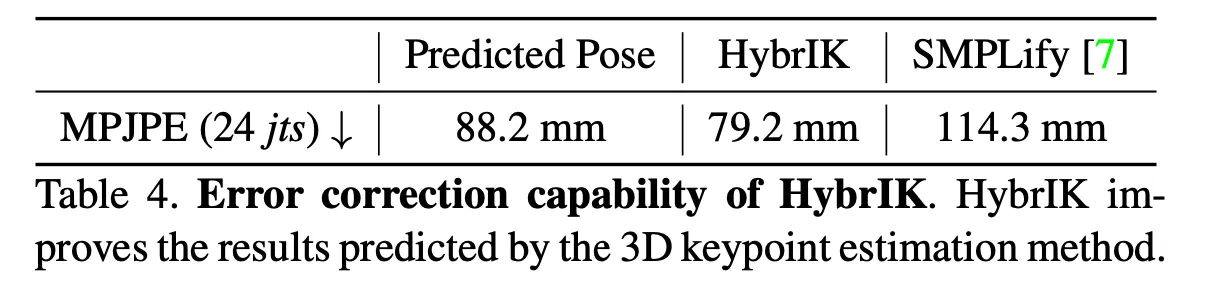
Error correction capability of HybrIK
•
HybrIK Algorithm의 오차 보정 능력 입증 실험
•
NeuralNet으로 3D Joint, Twist, Shape가 주어졌을 때, Error를 개선할 수 있는지 ?
•
비교군으로 SMPLify Method를 사용함
•
SMPLify는 Error를 늘린 반면, HybrIK은 Error를 줄여나감
◦
이 부분은 Unrealistic한 Pose를 보정해줄 수 있는 HybrIK 능력 덕분으로 추정됨
◦
우리 Architecture는 Single-Stage 3D Joint Estimation 방식이 무엇이든 상관 없기에 성능 상승의 여지또한 존재