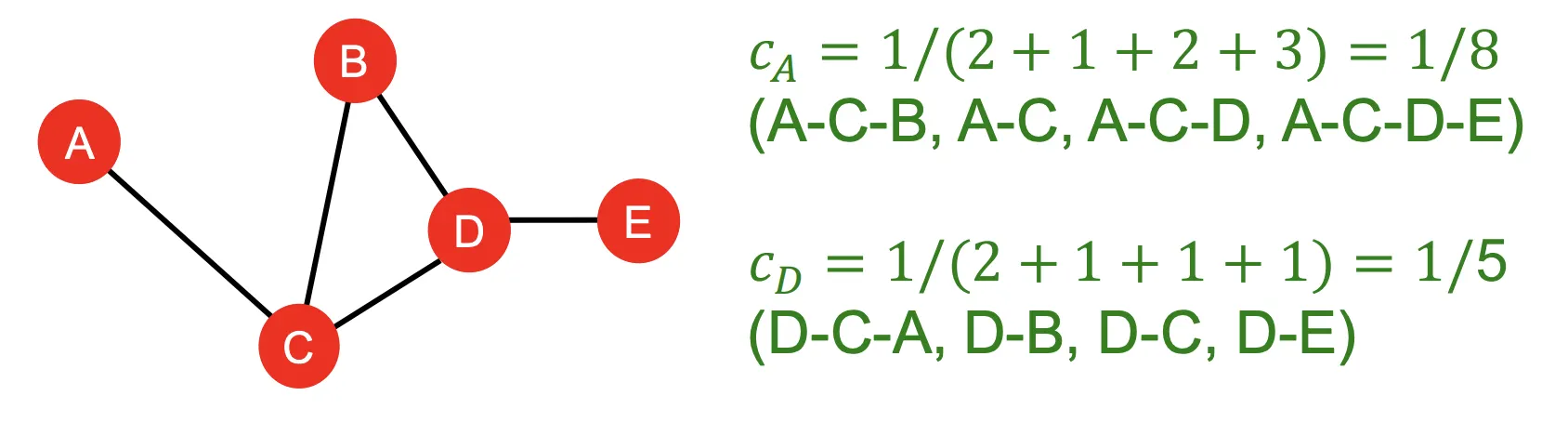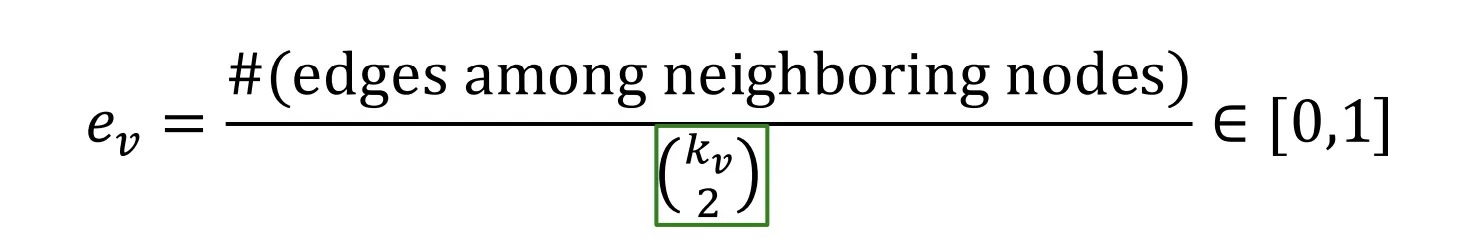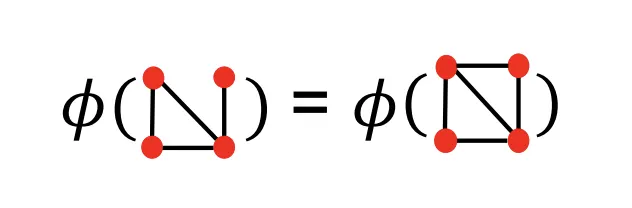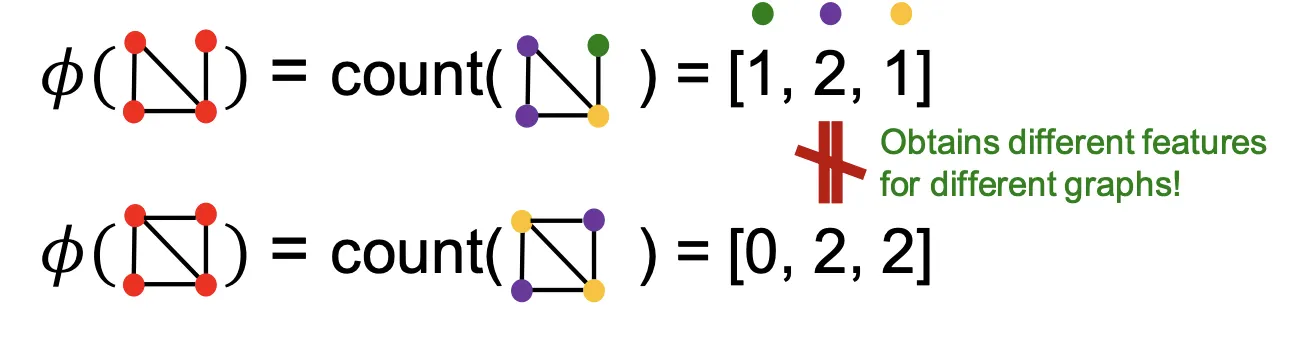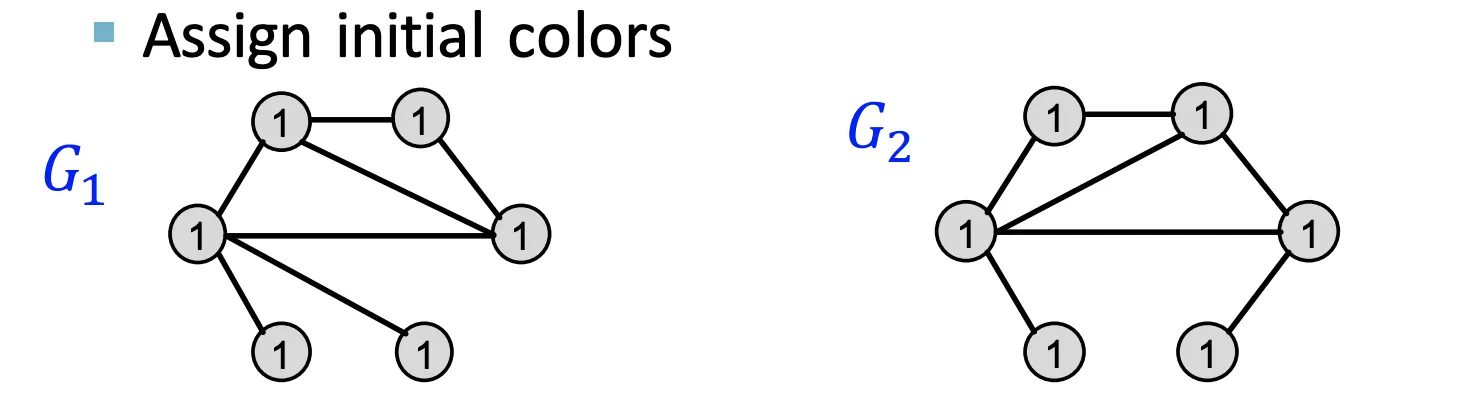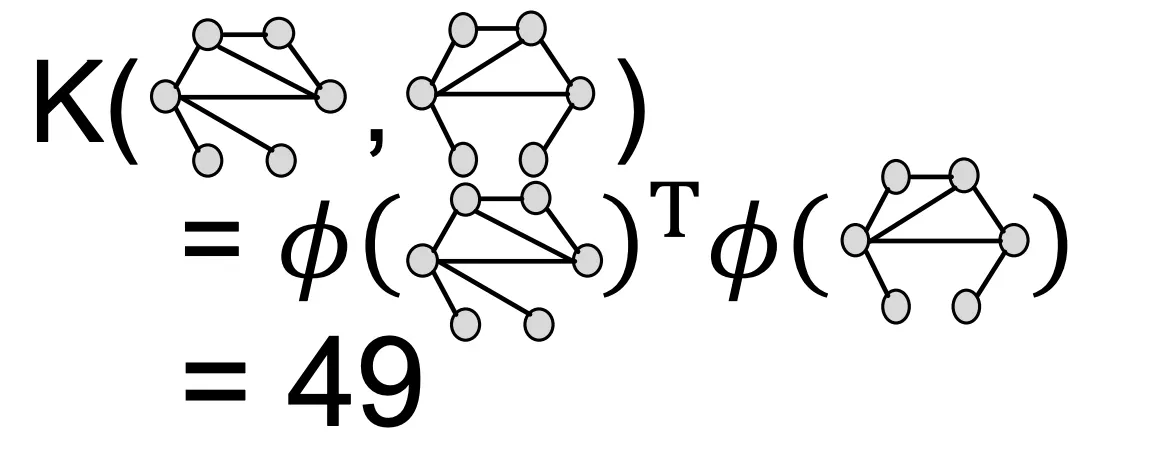Home
///
///
📈

강의 정리 : CS224w-Lecture 1~2

Lecture1. Machine Learning with Graphs

 Why Graph

What is Graph?
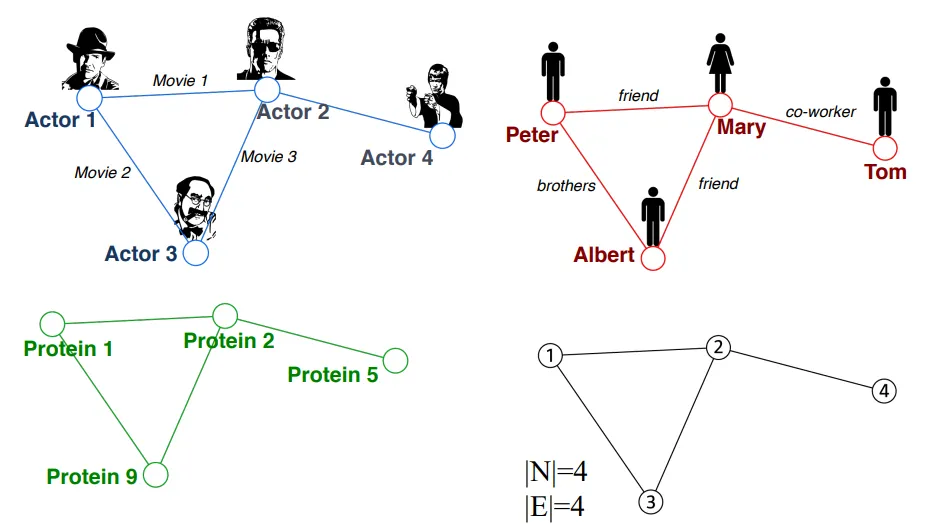
Graph는 Entity간의 관계와 상호작용을 설명하고 분석하기 위해 사용되는 일반적인 언어이다. 이는 각 레코드를 독립된 데이터 포인트로 생각하는게 아니라, 관계적인 측면에서 해석한다는 뜻이다.
Graph로 표현될 수 있는 도메인의 대표적인 예로는 컴퓨터 네트워크, 전염병 경로, SNS등이 있다. 이런 도메인을 Graph로 표현하면, Entity사이의 관계를 잘 캡쳐할 수 있다. 또 지식이나 사실을 Entity사이의 관계로 표현할 수 있는데 장면에 대한 설명(Scence Graph), 혹은 코드에 대한 추상적인 구조(Code Graph)등이 그 예이다.
CS224W에서 다룰 메인 주제는 Relational Structure(Graph)를 활용하여 어떻게 더 나은 Prediction을 하는가이다. 이 주제를 풀어서 얘기하면, Relational Structure를 가진 복잡한 도메인은 Graph로 표현이 가능하며 Graph를 이용해 이런 관계들을 명시적으로 묘사함으로서, 더 나은 Perforamance를 얻는다는 뜻이다.
Why is Graph Deep Learning Hard?
현대 딥러닝의 ToolBox는 단순한 시퀀스, 그리드같은 데이터 유형에 대해 특화되어 있다. 예를들어 텍스트나 음성은 선형적인 구조를 갖고 있고 이미지는 Fixed Size Grid 구조를 갖고있으며, 현대 딥러닝 모델들은 이러한 입력을 처리하는데 매우 뛰어나다 (RNN, CNN)
Graph는 훨씬 복잡한 구조를 가지고 있어 모델링이 어려운데, 예를 들면 다음과 같다.
1.
임의의 크기와 복잡한 Topology를 가지고 있다.
2.
고정된 기준점이나 순서가 없기때문에 Spatial Locality라는 개념이 없다.
3.
네트워크 자체가 종종 Dynamic하며, Multi-Modal Feature를 갖는다.
CS224W는 Graph같은 복잡한 데이터 유형에 대해 딥러닝 모델링을 하는 법에 대해 다루며, Graph에 대한 모델링은 실제로 아직도 개척중인 분야이다.
Deep Leaning in Graph
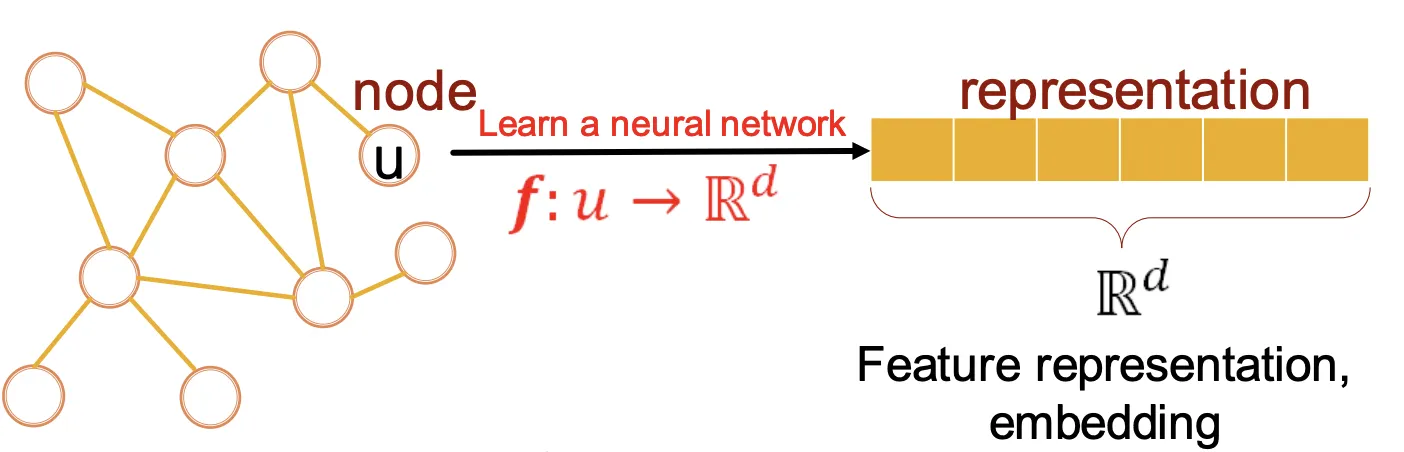
우리의 목표는 결국 Graph을 활용한 딥러닝 모델을 구축하는 것이다. 이때 입출력은 Node, Link, Generated Graph & Subgraphs 등이 될수 있는데, 어찌되었든 그 Task를 수행하는 NeuralNet을 어떻게 설계하느냐에 대해 다룬다. 즉 Feature Enginnering없이 바로 모델링 하는 과정을 주로 다룬다.
Feature Enginnering 과정을 없애기 위해 Graph의 Representation을 학습하는데, 이는 노드를 dd 차원으로 임베딩 함으로서 이루어진다. 임베딩이 잘 되면 DownStream Task에 쉽게 적용이 가능하므로 결국 우리의 목표는 Graph(Node, Grpah, Link등)을 dd차원으로 잘 임베딩 하는 것이다.
Course Outline
ML 전반과 Graph 데이터를 위한 Representation에 대해 다룰 예정이다. (1) 전통적인 방법론부터, (2) Node Embedding을 만드는 방법론, (3) Graph Neural Network에 대해 다루고, (4) Knowledge Graph와 (5) Grapah Grenrative Model, (6) 다양한 도메인으로의 적용에 대해 다룬다.

 Applications of Graph ML

Classic Graph ML Task
1.
Node Classification : Node의 속성을 예측하는 Task (Ex: Categorize Users/Items)
2.
Link Prediction : 2개의 Node사이에 놓친 관계가 있는지 예측하는 Task (Ex: Complete Knowledge-Graph)
3.
Graph Classification : 다른 Graphs들을 Categorize하는 Task (Ex: 분자 특성 Prediction)
4.
Clustering : Community형태의 Node들을 감지하는 Task (Ex: Social Circle Detection)
5.
Graph Generation, Graph Evolution..

 Choice of Graph Representation

Components of a (Graph)Network
(Graph)Network는 다음과 같이 구성되어있다.
1.
Object NN: Nodes(Vertices)
2.
Interatcions EE: Links, Edges
3.
System G(N,E)G(N,E): Network, Graph
Choosing a Proper Representation
문제와 데이터가 주어질 때 그것을 어떤식으로 표현하는지(Representation)가 이후 모델링에 큰 영향을 끼친다. 즉, 도메인/문제에 맞는 적절한 선택지를 고를 수 있는 능력이 곧 네트워크를 성공적으로 사용할 수 있는 능력이다.
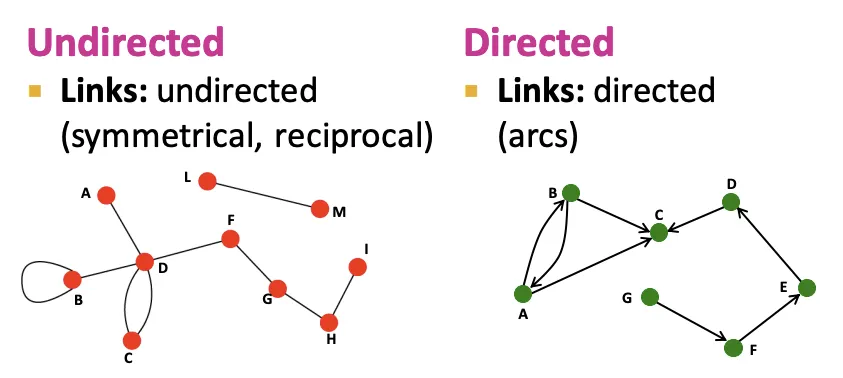
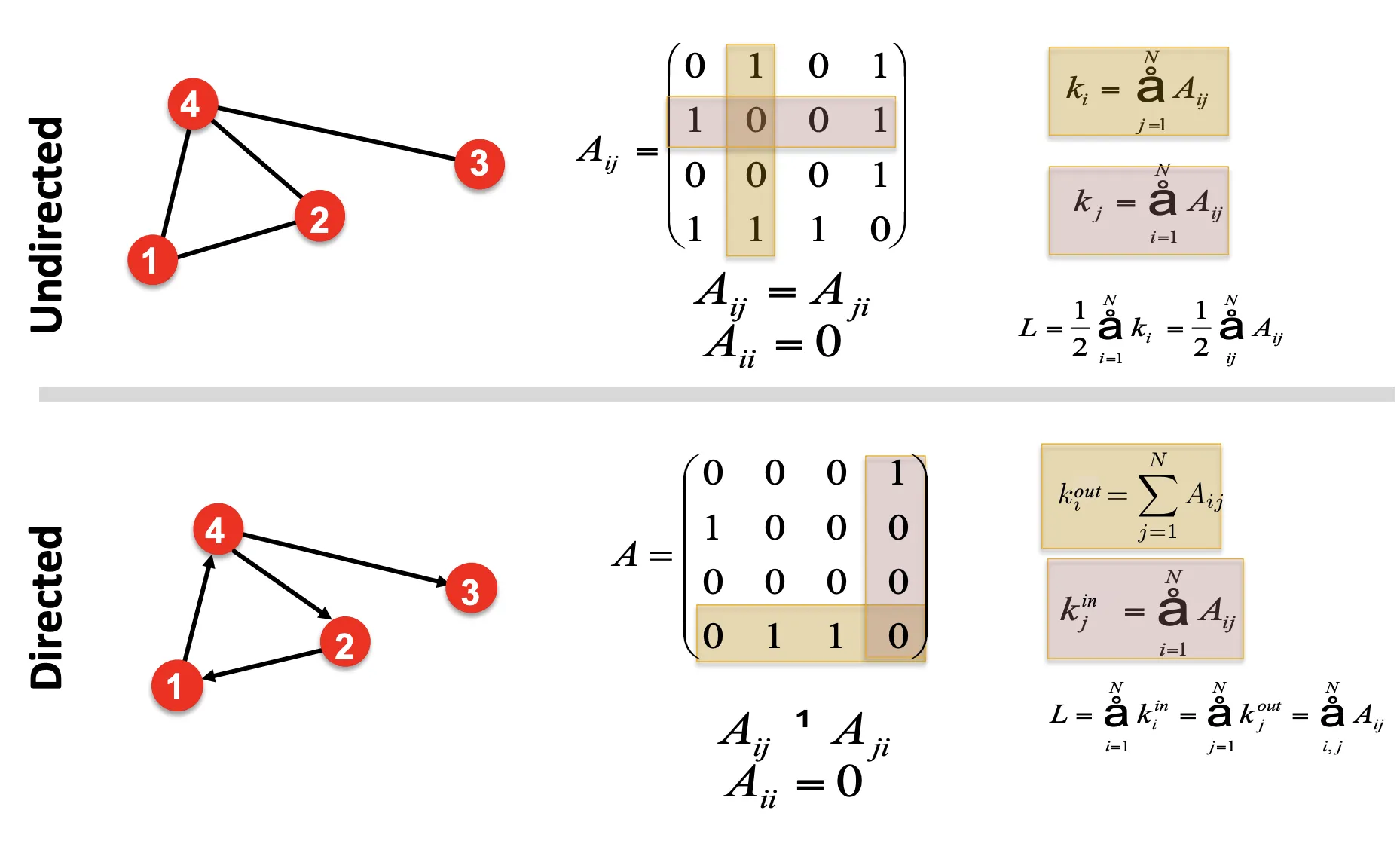
Definition : Undirected vs Directed
Node Degrees : Undirected vs Directed
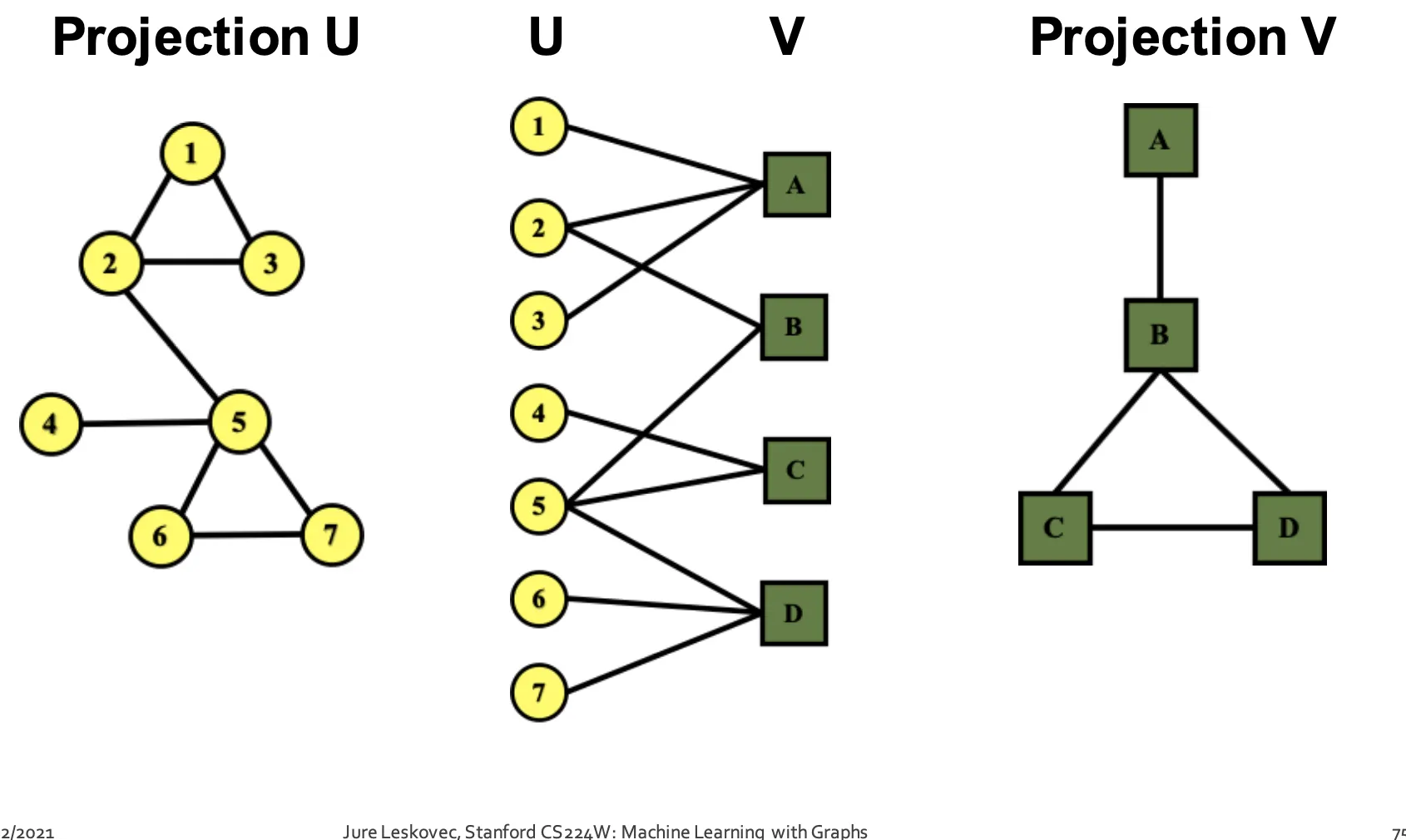
Bipartite Graph
•
모든 Link가 분리된 Set (U,VU,V)간에서만 이루어지는 Graph이다.
•
(저자-논문), (배우-영화), (재료-요리)등이 자연적인 Bipartite Graph의 예이다.
•
한 쪽 Set만 이용해서 Folded(Projected) Graph를 만들 수도 있다.
Representing Graph
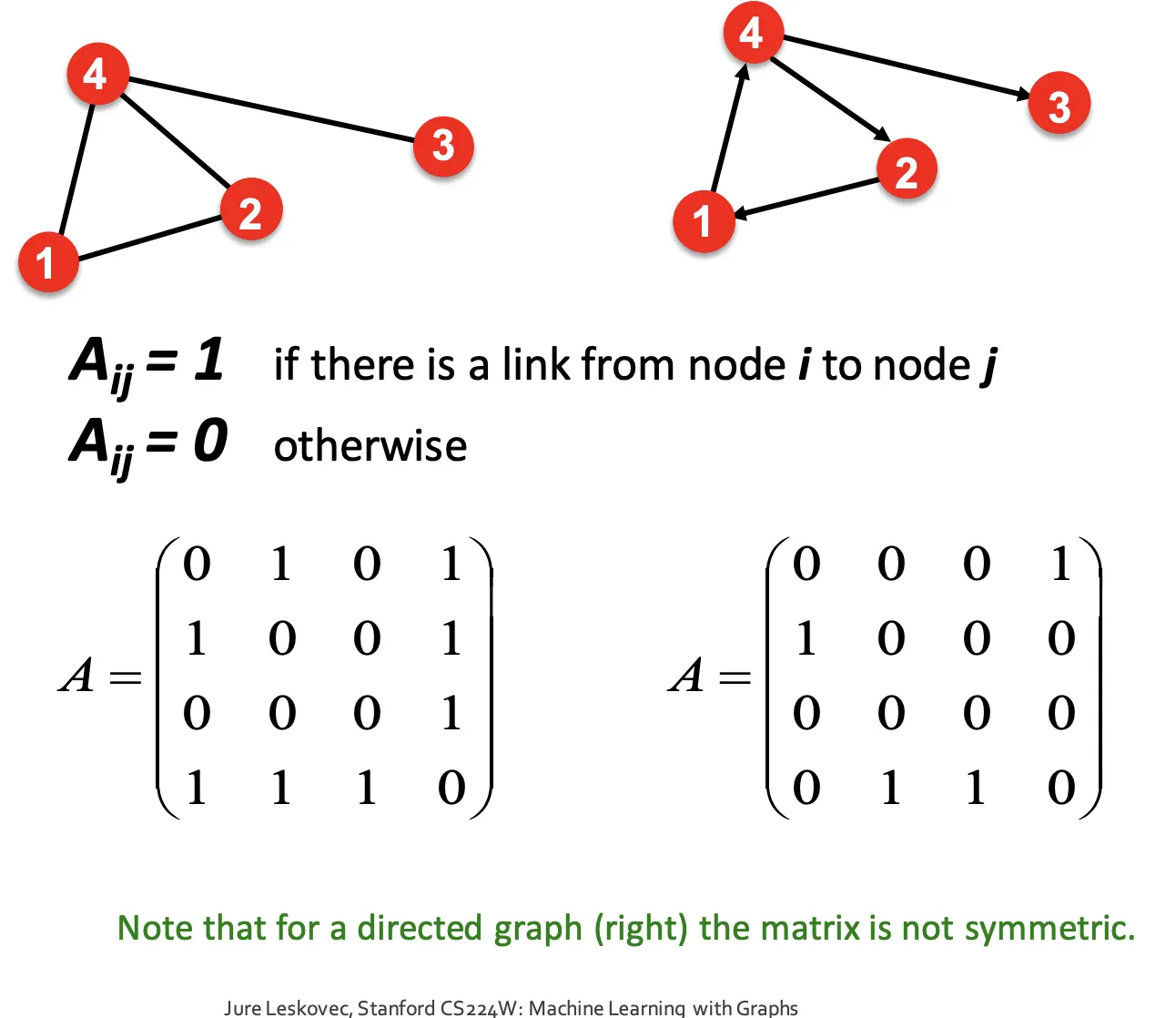
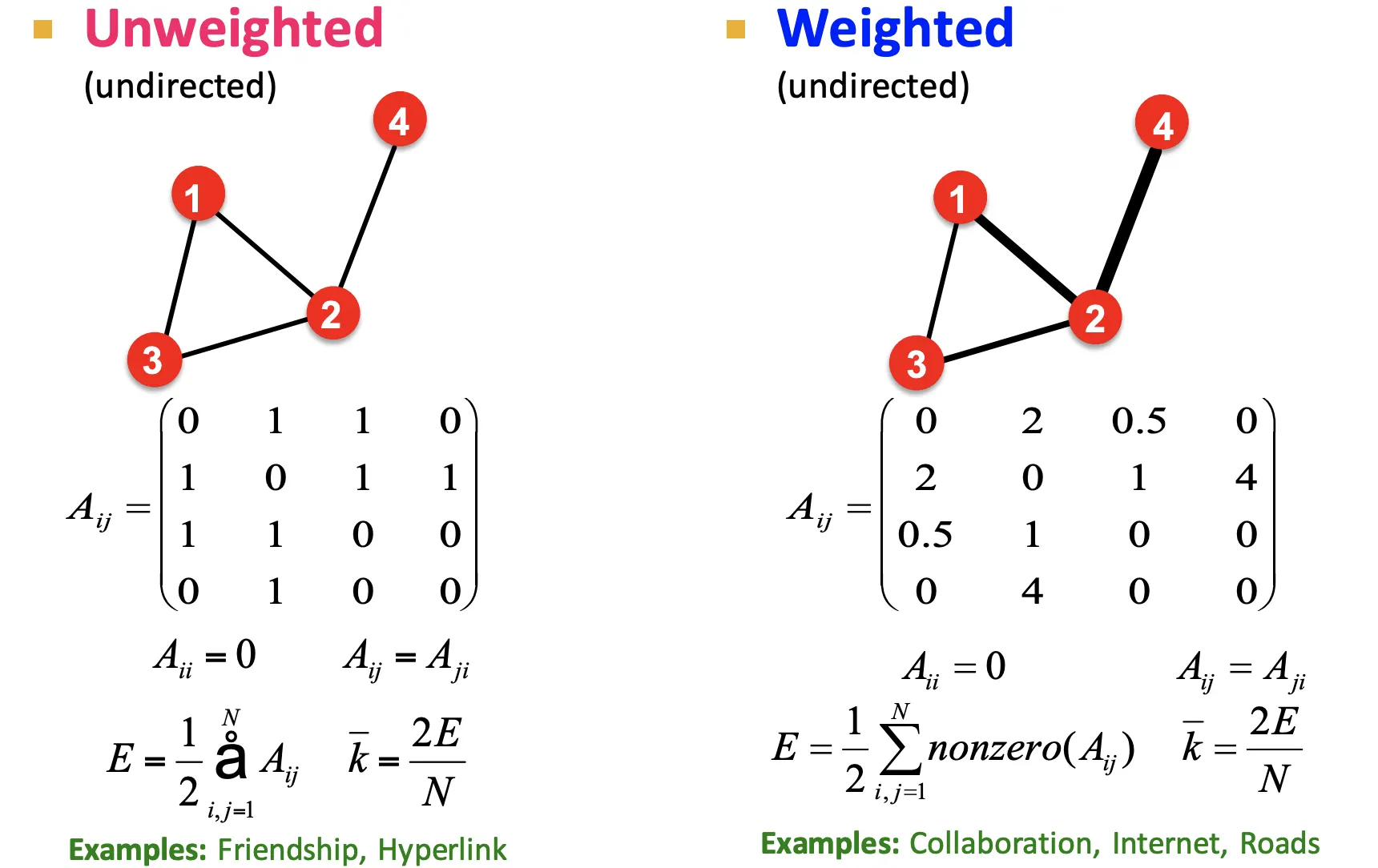
그래프를 수식적으로 나타내는 방법도 다양하다. 대표적인 방법은 Adjacency Matrix로 나타내는 것이다.
Adjacency Matrix
Node의 갯수가 nn 일때, n×nn \times n 행렬 AA 를 만들고, 대응되는 위치의 노드가 연결 되어있으면 1, 아니면 0으로 표시한다. Undirected의 경우 Symmetric하다.
Adjacency Matrix는 연산이 편리하다는 장점 (Ex:연결된 Node의 합을 행, 열합으로 구할 수 있다)이 있으나, 극도로 Sparse 하다는 단점이 있다.
Edge List
2차원 행렬로 Graph를 표현하는 방식이다. 간단해서 딥러닝 프레임워크에서 인기있는 표현방식이다. 그러나 그래프의 연산이 불편해 조작이나 분석이 어렵다.
Adjacency List
Graph가 크고, Sparse할 경우에 사용하기 좋다. 각 Node의 이웃의 목록 형식으로 표현하는 방식이다.
Node and Edge Attributes
Graph의 각 개체는 속성을 가질 수 있다, 사람사이의 관계를 예로 들면, Node즉 사람은 성별, 관심사, 위치 등의 속성을 가질 수 있고, Link는 호의적인지, 친한지, 어떤관계인지 등의 속성을 가질 수 있다.
즉, 단순히 Graph의 Topology 뿐만아니라 이들이 갖고있는 속성까지 고려하여 모델링 해야한다.
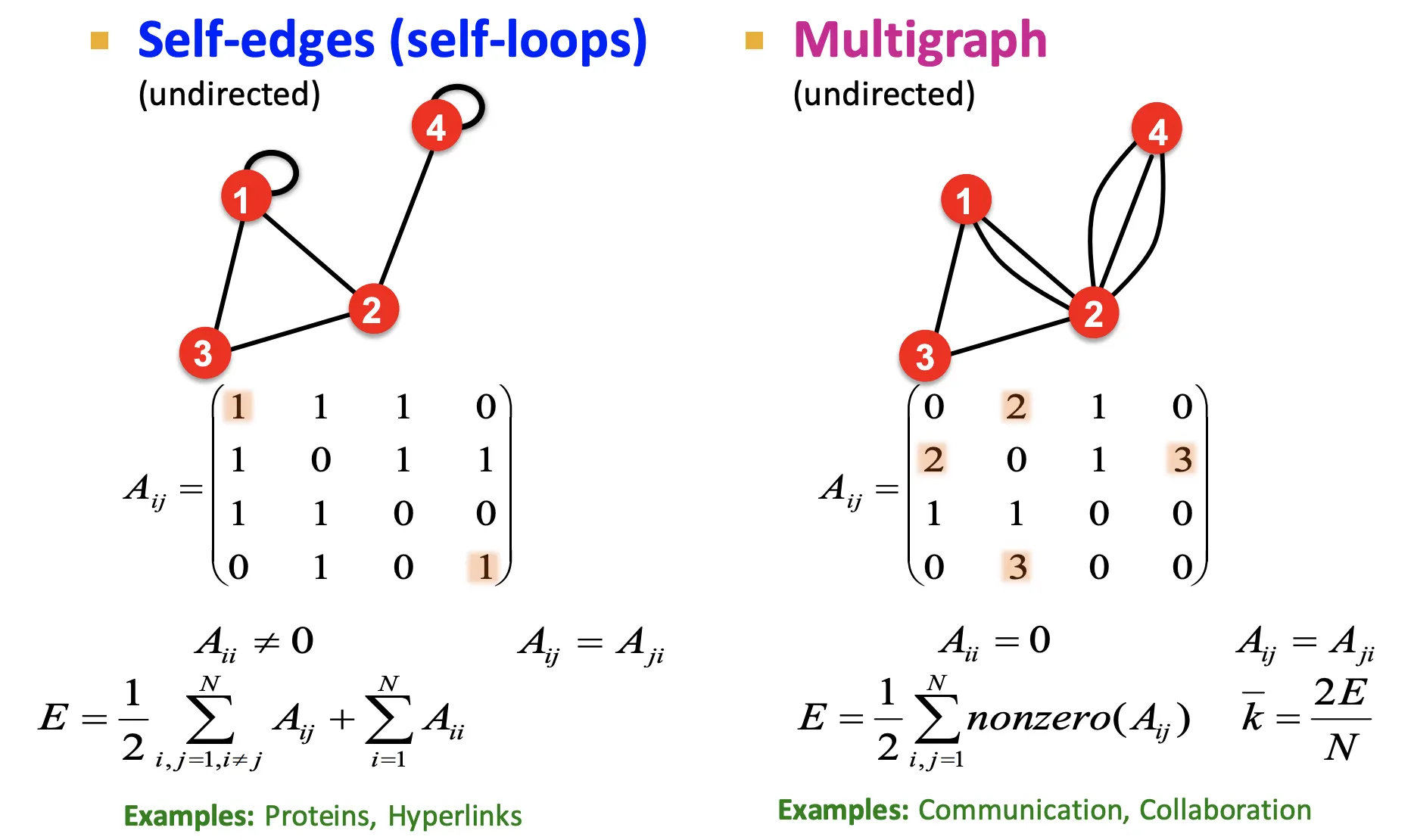
More Types of Graphs
속성을 Representation 자체에 녹여낼 수도 있다.
•
연결 강도를 Adjacency Matrix에 포함시킬 수 있다.
•
Self-Loop나 Node간의 중복된 Link를 허용하는 Graph도 Adjacency Matrix에 포함시킬 수있다.

Lecture2. Traditional Methods for Machine Learning in Graphs

Traditional ML Pipeline
Traditional ML Pipeline은 크게 2단계로 이루어져 있다.
1.
Data Point, Node, Link, Graph(이하 입력)를 Feature Vector로 변환해 ML모델을 학습시킨다.
2.
새로운 입력이 들어오면 Feature Vector를 얻고 모델을 통해 예측한다.
Lecture Object : Feature Design
Goal : 입력 Set이 주어졌을때 예측값을 만들어내는것 / 모델은 ML Model 사용
Design Choice
•
Feature : dd차원의 벡터
•
입력 : Nodes, Links, Sets of Nodes, Entire Graph
•
Objective Function : 무슨 Task를 풀려고 하는가?
1.
Traditional ML Pipeline은 수작업으로 만들어진(Hand-Designed) Feature를 사용한다.
2.
Hand Designed Feature를 Graph의 세 레벨 (Node, Link, Graph)로 나누어 설명한다.
3.
Undirected Graph를 중점으로 설명한다.

 Traditional Feature-Based Method : Node

Goal : Network에서 Node의 구조와 위치를 특정할 수 있는 Feature를 만드는 것
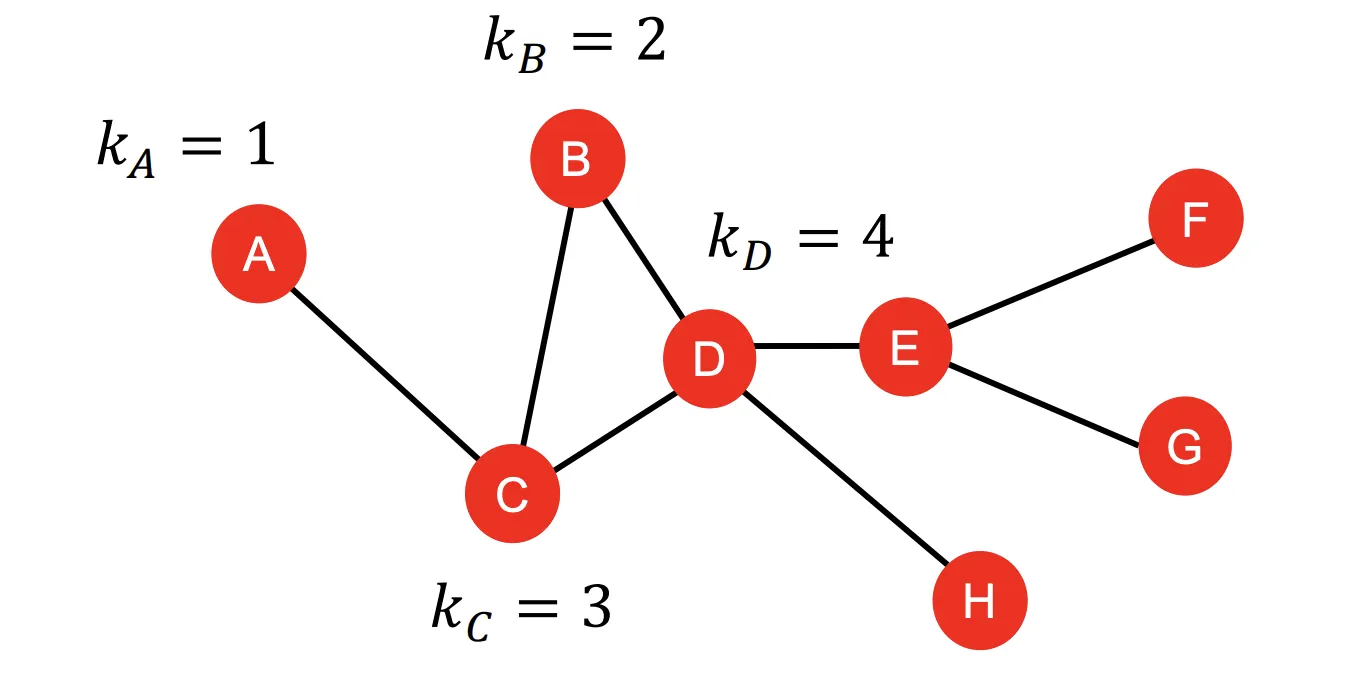
1. Node Degree (kvk_v)
Node vv의 Degree를 kvk_v라고 정의하자. 이때 kvk_v는 vv가 갖고있는 Edge(Link)의 수와 같다.
2. Node Centrality(cvc_v)
Node Degree는 단순히 이웃한 Node의 갯수를 세므로, 그것들의 중요도를 Capture할 수 없다.
Node Centrality(cvc_v)는 Graph에서 해당 Node(v v)의 중요도를 포함시킨 개념이다.
•
2-1. Engienvector centrality
◦
Important : vv가 Important 이웃노드 uu에 둘러싸여 있을 때 vv는 Important하다고 한다.
◦
Formula
▪
cv=1λ∑u∈N(v)cuc_v = {1 \over \lambda} \sum\limits_{u\in N(v)}c_u (λ\lambda는 Normalization 상수) ⇒ 이렇게 하면 Recursive함
▪
λc=Ac\lambda c= Ac (AA는 Adjacency Matrix)
•
고유값과 고유벡터 형태로 재설정
•
cc는 AA의 고유벡터, λ\lambda는 고유값이며 λmax\lambda_{max}는 항상 양수에 Unique함
•
2-2. Betweenness centrality
◦
Important : vv가 다른 노드들을 연결하는 최단 경로에 있을때 Important하다고 한다.(경유)
◦
Formula : cv=∑s≠v≠tv를 포함하는s와 t사이 최단 경로s와 t사이 최단 경로c_v = \sum\limits_{s \neq v \neq t}{v를\ 포함하는 s와\ t사이 \ 최단\ 경로 \over s와\ t사이\ 최단\ 경로}
•
2-3. Closeness Centrality
◦
Important : vv가 다른 모든 노드에 대한 최단 경로의 길이가 짧을때 Important하다고 한다.
◦
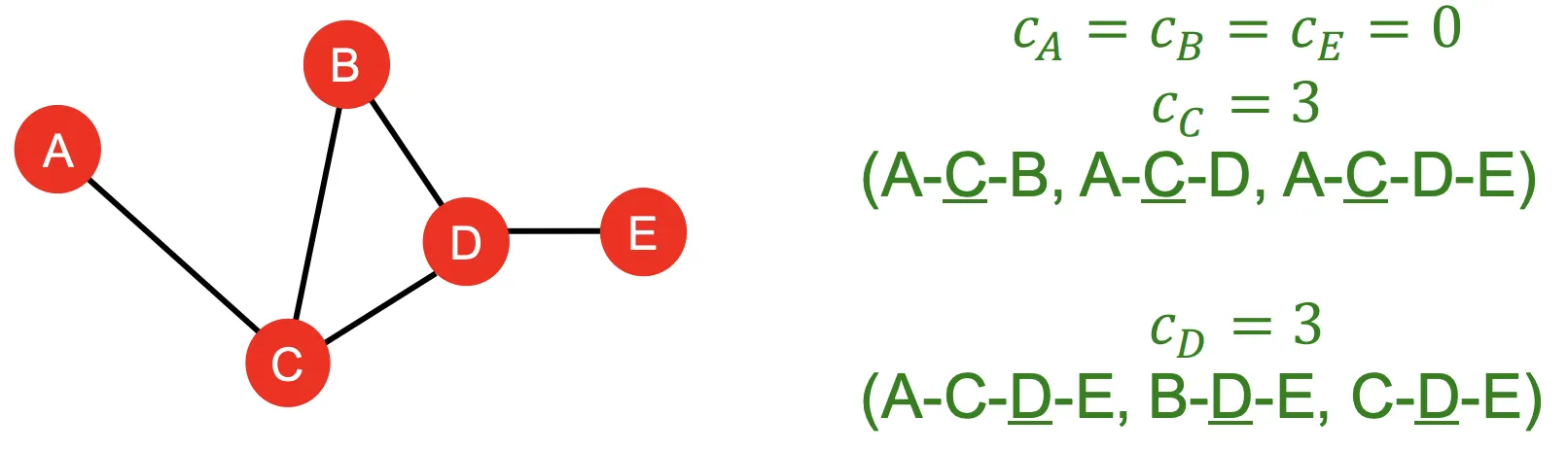
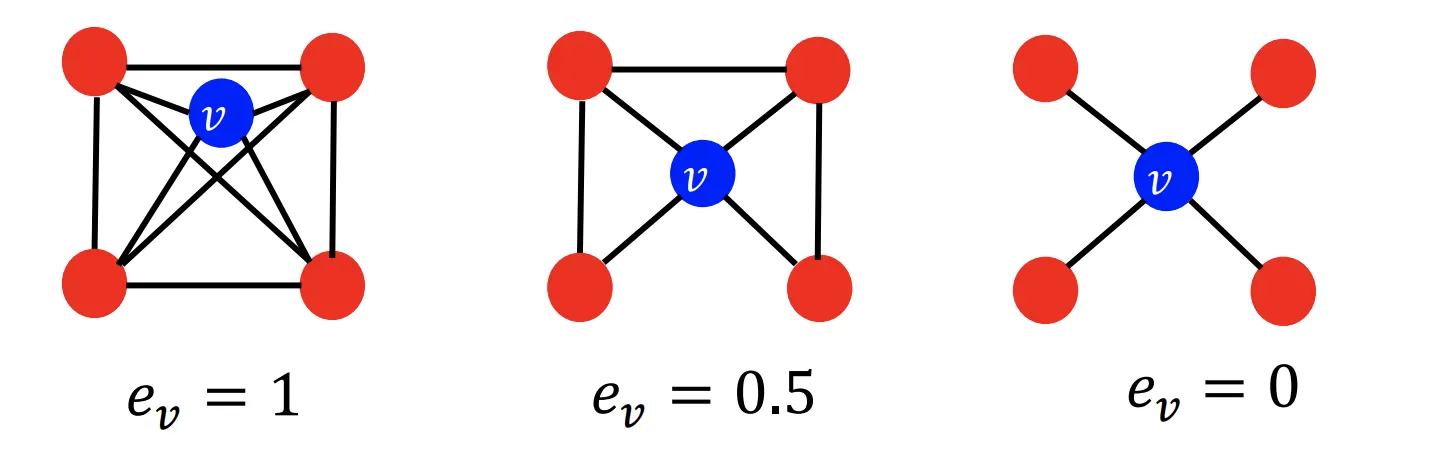
Formula : cv=1÷∑u≠v(u와 v사이의 최단경로의 길이)c_v = 1 \div \sum\limits_{u \neq v} (u와\ v사이의\ 최단경로의\ 길이)
3. Clustering Coefficient
Clustering Coefficient는 Node vv의 이웃들이 얼마나 연결되어 있는지를 측정하는 개념이다.
vv의 이웃간 연결된 경우의 수를 이웃 Node들이 서로 연결될 수 있는 전체 경우의 수로 나누어준다.
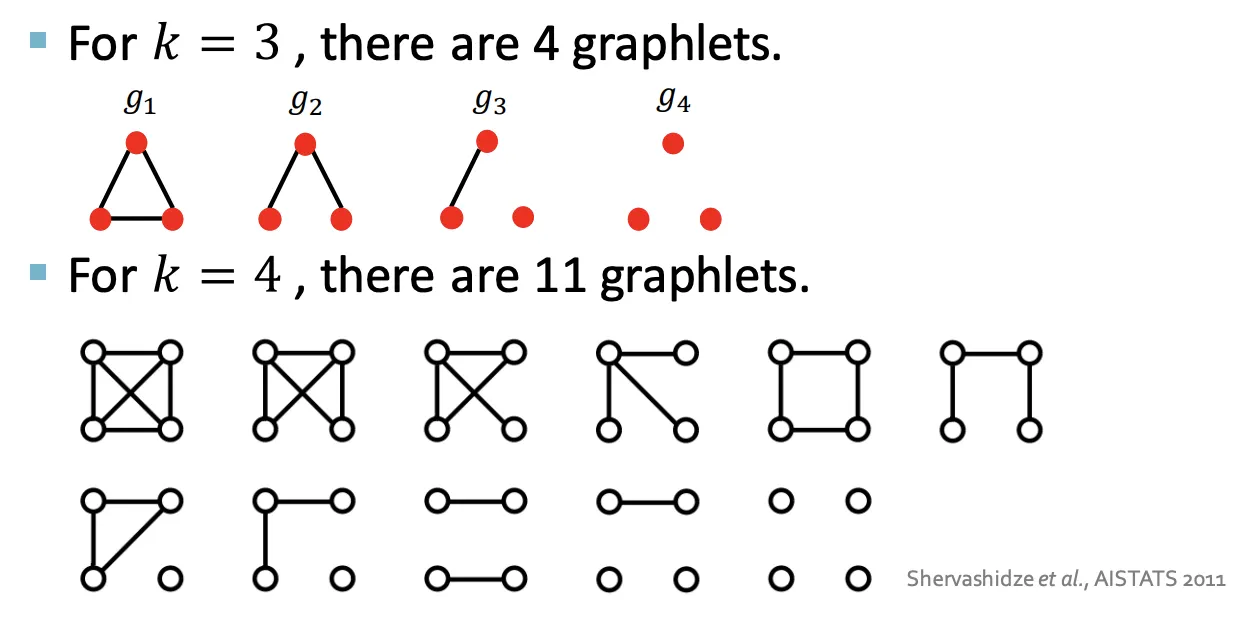
4. Graphlets
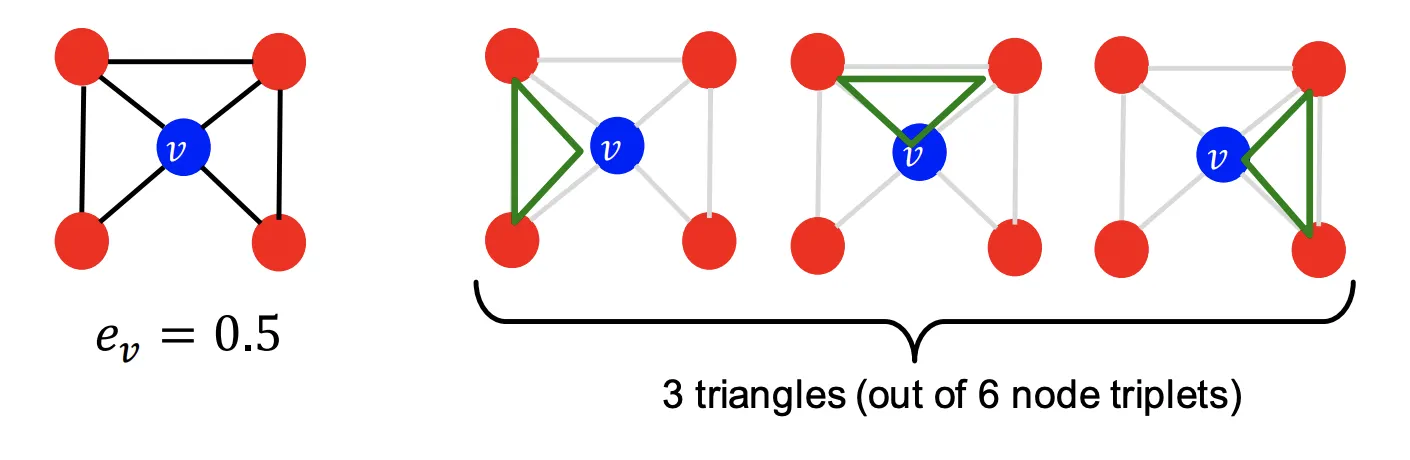
Observation : Clustering Coefficient는 Ego-Network의 #(Triangle)을 센다)
•
Ego-Network : Node가 주어졌을때 자기자신과 1차-이웃만 포함한 Network
•
#(Triangle) : 3개의 노드가 연결되어 있는 것
•
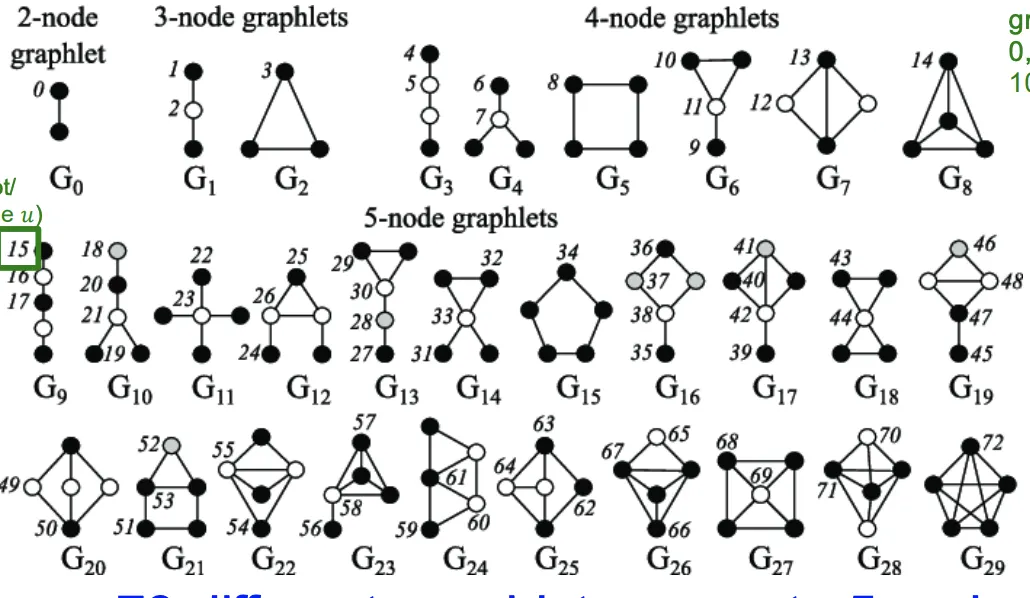
이런 Triangle Counting을 다양한 구조에 대해 일반화 하는것 ⇒ Graphlets의 개념
•
Graphlet의 목적 : Node uu의 이웃 구조를 기술하는 것
◦
Graphlets : uu의 이웃 구조를 기술하기 위한 작은 Subgraph(Template?)
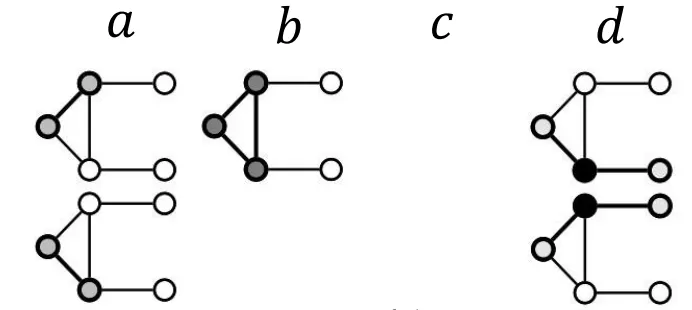
Graphlet Degree Vector(GDV) : Node의 Graphelt-Based Feature
•
Degree of Graphlet : 특정 Node가 포함된 Graphlet의 갯수 벡터이다. 어떻게 세는지는 아래의 예시를 통해 설명한다.
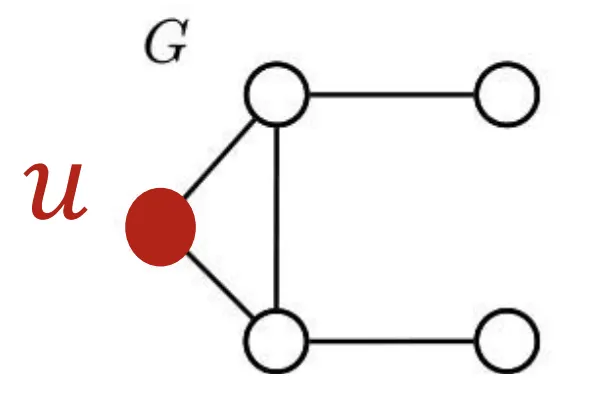
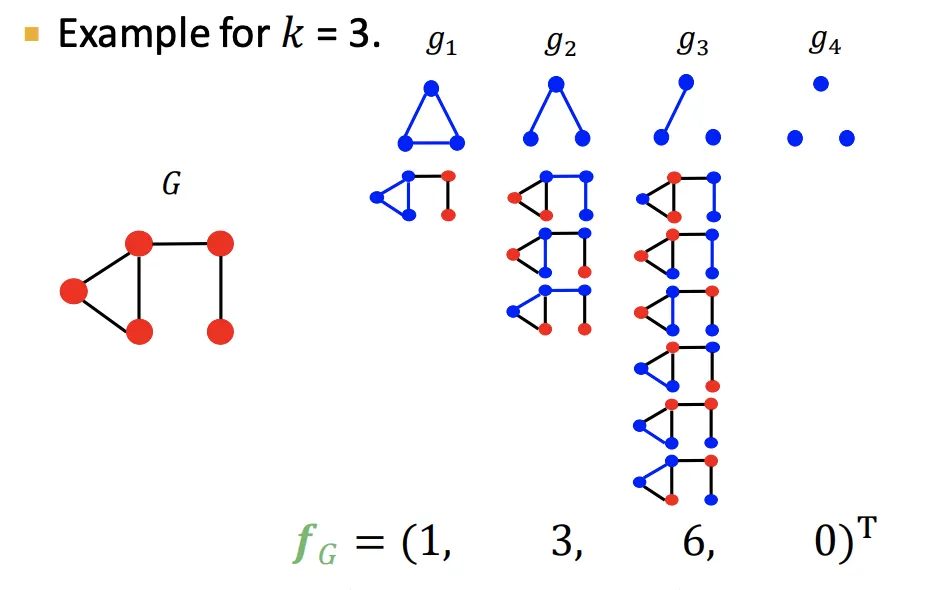
1.
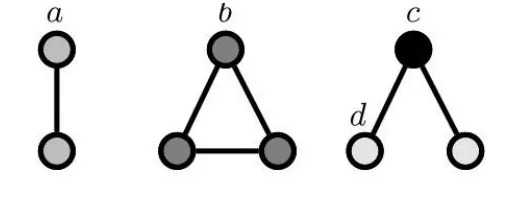
아래와 같이 생긴 Graph GG에서 Node uu에 관심있다고 가정해 보자.
2.
Graph 구조를 보았을때, 최대 3개의 Node가 참여하는 Graphlet을 만들 수 있다.
3.
각각의 Graphlet이 GG에서 uu를 포함한채로 몇번 나타나는지 세보자
4.
Node uu의 GDV는 [2,1,0,2]가 된다.
Graphlet Summary
2~5개의 Node가 참여하는 Graphlet의 갯수는 73개이다. 이를 73차원의 벡터로 표시할 수 있고, 각 Index는 특정한 Neighborhood Topology에 Signature이다. 이 벡터를 이용해 Node의 Local Network Topology를 잘 정제된 Feature로 만든게 GDV이며, 앞에서 소개한 방식보다 자세한 정보를 갖고있다.
Node-Level Feature Summary
Node Level Feature는 2가지 분류로 나눌수 있다
1.
Importance Based (Ex Task : 영향력있는 Node찾기(SNS의 셀럽찾기))
a.
Node Degree : 단순히 이웃의 숫자를 센다
b.
Node Centrality : Graph에서의 이웃 노드의 중요도를 모델링한다.
2.
Structure Based (Ex Task : Node의 역할 찾기(단백질 구조에서 특정 단백질의 기능찾기))
a.
Node Degree : 단순히 이웃의 숫자를 센다
b.
Clustering Coefficient : 이웃이 어떻게 연결되어있는지 측정한다.
c.
Graphlet Count Vector : 여러 Graphlet들이 출현하는 빈도를 센다.

 Traditional Feature-Based Method : Link

Link-Level Prediction Task
Link-Level Task는 존재하는 Link를 바탕으로 새로운 Link를 예측하는 것이다. Link를 예측하는 Task는 크게 2가지 Formulation이 있다.
1. 랜덤하게 사라진 Link 찾기 : Static한 Graph에 적절하다.
2. 시간이 흐름에 따라 생겨나는 Link 찾기 : SNS, Transaction같이 Dynamic한 Graph에 적절하다.
Link-Level Prediction의 자세한 방법은 다음과 같다.
1.
각 Node쌍 (x,y)x,y)에 score c(x,y)c(x,y)를 계산한다.
2.
c(x,y)c(x,y) 내림차순으로 Node 쌍을 정렬한다
3.
Top NN개의 Pair들을 새로운 Link로 예측한다.
Link - Level Feature : Distance-Based Features
1. 노드간 최단 경로
두 Node간 최단경로의 거리를 사용한다. 이웃의 수나 강도에 대한 어떠한 정보도 캡쳐하지 않는다.
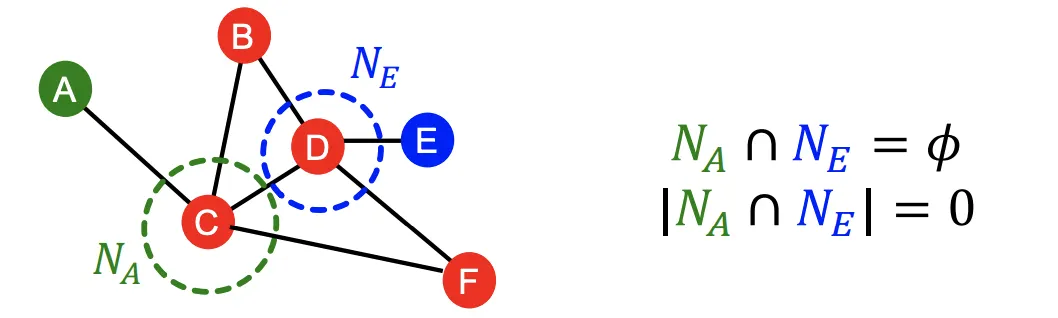
2. Local Neighborhood Overlap
두 Node가 공유하는 이웃을 캡쳐한다.
•
Coomon Neighbors : 단순히 교집합을 구한다
•
Jaccard’s Coefficient : 교집합의 크기를 합집합으로 나눈다
•
Adamic-Adar Index : (SNS에서 잘 동작한다고 하네요) 두 Node가 공유하는 이웃을 u라고 할 때 ∑u1log(ku)\sum \limits_u {1\over log(k_u)}
3. Global Neighborhood Overlap
Local Neighborhood Overlap의 단점은 잠재적 이웃도 직접적인 공통 이웃이 없으면 0이 된다는 점이다.
•
Katz Index : 주어진 Node 쌍을 잇는 모든 길이의 경로를 센다. Matrix를 이용해 깔끔하게 연산할수 있다.
◦
AuvA_{uv}는 직접 이웃일 때 1이고 아니면 0이다.
◦
Puv(K)P_{uv}^{(K)}는 KK길이의 u,vu,v를 잇는 경로이다.
◦
P(K)P^{(K)} = AkA^k이다.
◦
Formula
▪
Suv=∑l=1∞βlAuvlS_{uv} = \sum \limits_{l=1}^\infty \beta^l A_{uv}^{l} (ll : Path의 길이, β\beta: Discount Factor(0<β<10<\beta<1)
▪
Suv=∑l=1∞βlAi=(I−βA)−1−IS_{uv} = \sum \limits_{l=1}^\infty \beta^lA^i=(I-\beta A)^{-1}-I (Closed-Form)
Node-Level Feature Summary
Node Level Feature는 3가지 분류로 나눌수 있다
1.
Distance-Based :두 Node간 최단경로의 거리
2.
Local Neigborhood Overlap : 두 Node가 공유하는 이웃의 수
3.
Global Neighborhood Overlap : 두 Node를 잇는 모든 길이의 경로 가중합

 Traditional Feature-Based Method : Graph

Goal : 전체 Graph 구조를 특정할 수 있는 Feature를 만드는 것
•
아이디어 : Graph로 Feature를 직접 만드는 대신 Kernel을 만들자.
◦
Kernel K(G,G′)∈RK(G,G') \in \R 은 두 Graph(G)(G) 사이의 유사도를 측정한다.
◦
Kernel Matrix는 항상 양의 고유값을 갖고 대칭행렬 이어야한다.
◦
Feature Representaiton ϕ(.)\phi(.)이 존재한다.
◦
이 Kernel을 SVM등에 붙여서 사용한다.
Kernel Method
•
Goal : Graph Feature Vector ϕ(G)\phi(G)를 설계한다
•
Idea : Graph에 대해 Bow를 만든다.
◦
Bow : NLP에서 모든 단어가 몇 번 나타나는지 세는 방법
◦
Naive Solution : Node를 Word로 사용한다. 그러나 너무 Naive해서 써먹기 어렵다.
◦
Node Degrees : Node Degree를 Word로 사용한다.
◦
이런식의 Bag-of-something 방식이 Graphlet Kernel과 WL Kernel에서도 사용된다.
Grahplet Features
•
Idea : Graph에 존재하는 서로 다른 Graphlet의 숫자를 세자
•
Note : 이때의 Graphlet은 Node-Level과 조금 다른 정의를 갖고있다.
◦
Isolated Node로 Graphlet의 일부로 허용한다.
◦
Root Node가 없다.
•
Graph GG와 Graphlet list gk=(g1,g2...gnk)g_k = (g_1,g_2 ...g_{nk})가 주어졌을 때 Graphlet Count Vector fG∈Rnkf_G \in \R^{nk} 는 Graph에서 나타나는 각 Graphlet의 인스턴스 수로 정의된다.
◦
(fG)i=#(gi∈G)(f_G)_i = \#(g_i \in G) | (for i=1,2,...nk)i = 1,2,...n_k)
Graphlet Kernel
•
2개의 Graph GG 와 G′G'가 주어지면, Graphlet Kernel은 K(G,G′)=fGTfG′K(G,G') = {f_G}^Tf_{G'}로 표현될 수 있다(내적)
•
Problem : GG 와 G′G'가 크기(Scale)이 다르면 값이 크게 왜곡된다.
•
Solution: fGf_G 대신 Sum으로 나눠준 hGh_G를 사용한다. hG=fGSum(fG)h_G = {f_G \over Sum(f_G)}
•
Limitation : Graphlet을 세는 연산이 매우 Expensive하다 !
◦
nn 크기의 Graph의 kk 크기의 Graphlet를 세려면 nkn^k번 연산해야 한다.
Weisfeiler-Lehman Kernel
•
Goal : 효율적인 Graph Feature Descriptor를 만드는 것
◦
WL-Kernel은 강력하고 효율적이어서 인기가 많다.
•
Idea : Node Degree를 이용해 반복적으로 Node Vocap을 풍부하게 만들어 나가는 것
◦
One-Hop Neighborhood인 Node Degree 방식을 일반화 한 버전이다.
◦
Color Refinement 알고리즘을 통해 이루어진다.
•
각 Step에서의 Time-Complexity가 Edge에 따라 Linear하게 증가한다.
Color Refinement
•
Given : Graph GG와 그것들의 Set of Nodes VV
1.
Initial Color c(0)(v)c^{(0)}(v)를 각 노드 vv에 할당한다
2.
Iteratively하게 Node의 Color를 정제해 나간다. c(k+1)(v)=HASH({c(k)(v),{c(k)(u)}u∈N(v))c^{(k+1)}(v) = HASH(\{c^{(k)}(v), \{c^{(k)}(u) \}_{u\in N(v)})
•
HASH는 다른 입력을 다른 Color로 매핑하는 연산이다.
3.
KK Step 동안의 정제가 끝나면 c(K)(v)c^{(K)}(v) 값을 Summary한다.
◦
비슷하지만 조금 다른 Graph 두개 (G1,G2G_1, G_2)가 주어졌을때 Color Refienment 예시이다
1.
동일한 Initial Color를 모든 Node에 할당한다.
2.
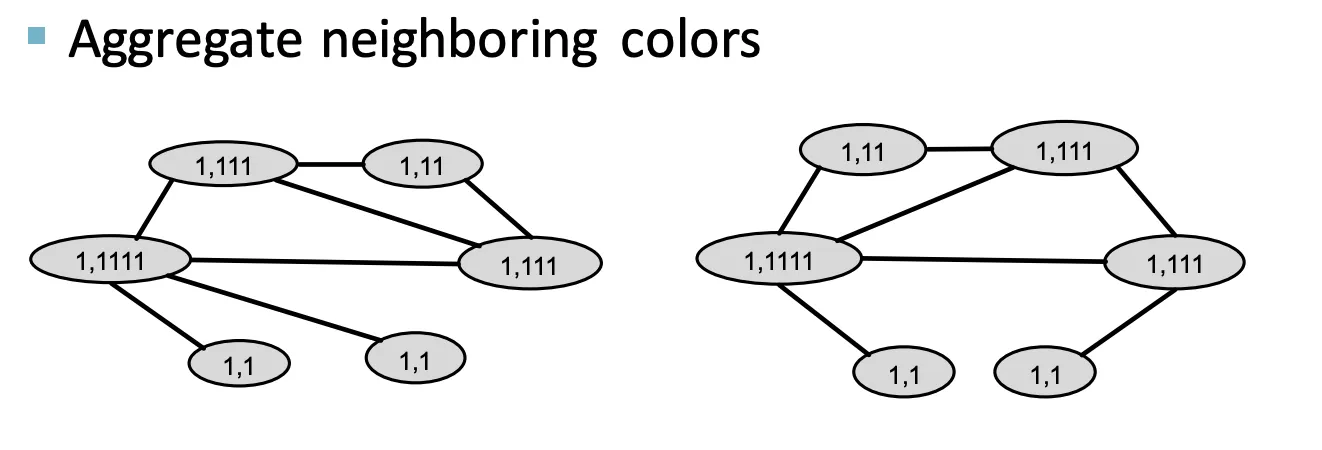
이웃하는 색상에 대해 Aggregate한다.
3.
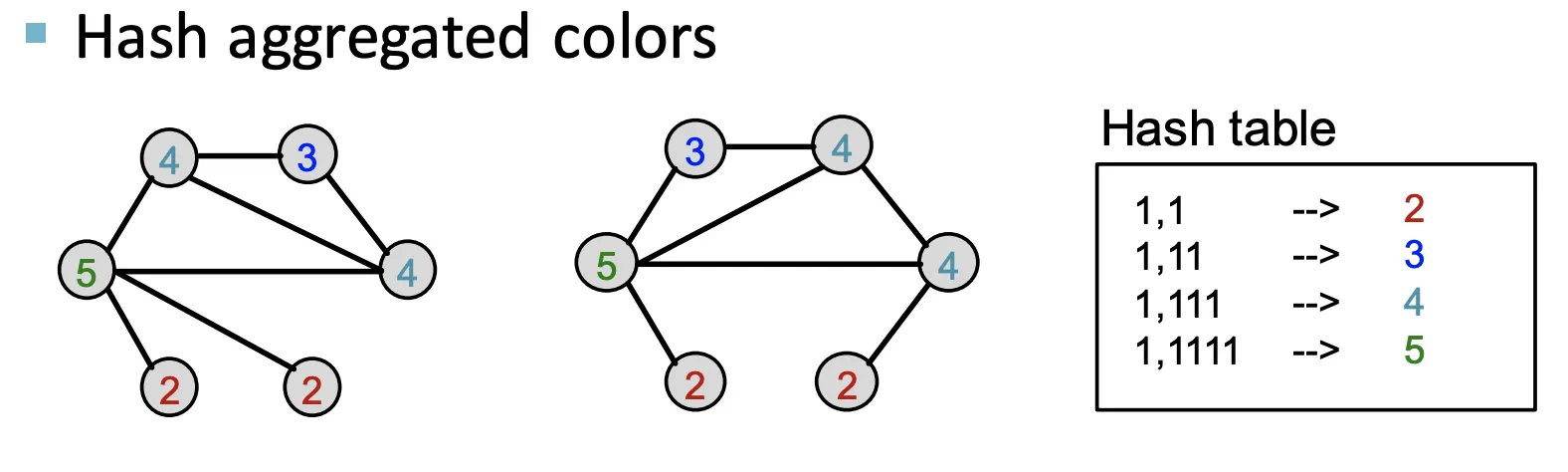
Aggregate된 Color를 HASH한다.
4.
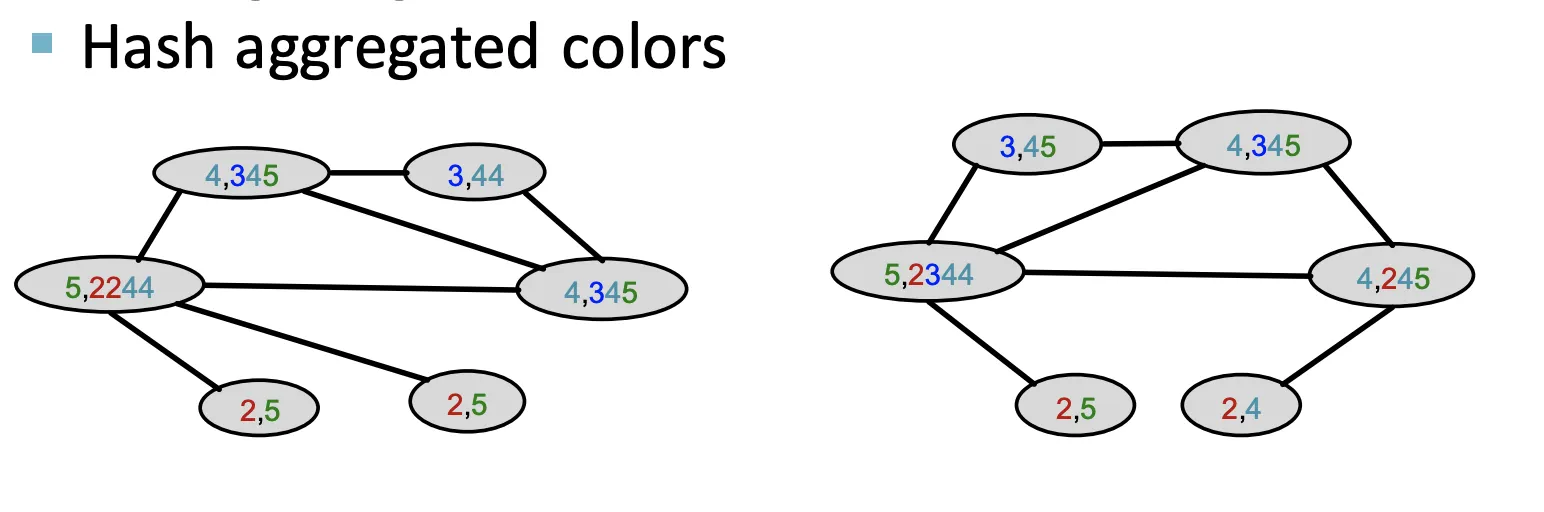
이웃하는 색상에 대해 Aggregate한다.
5.
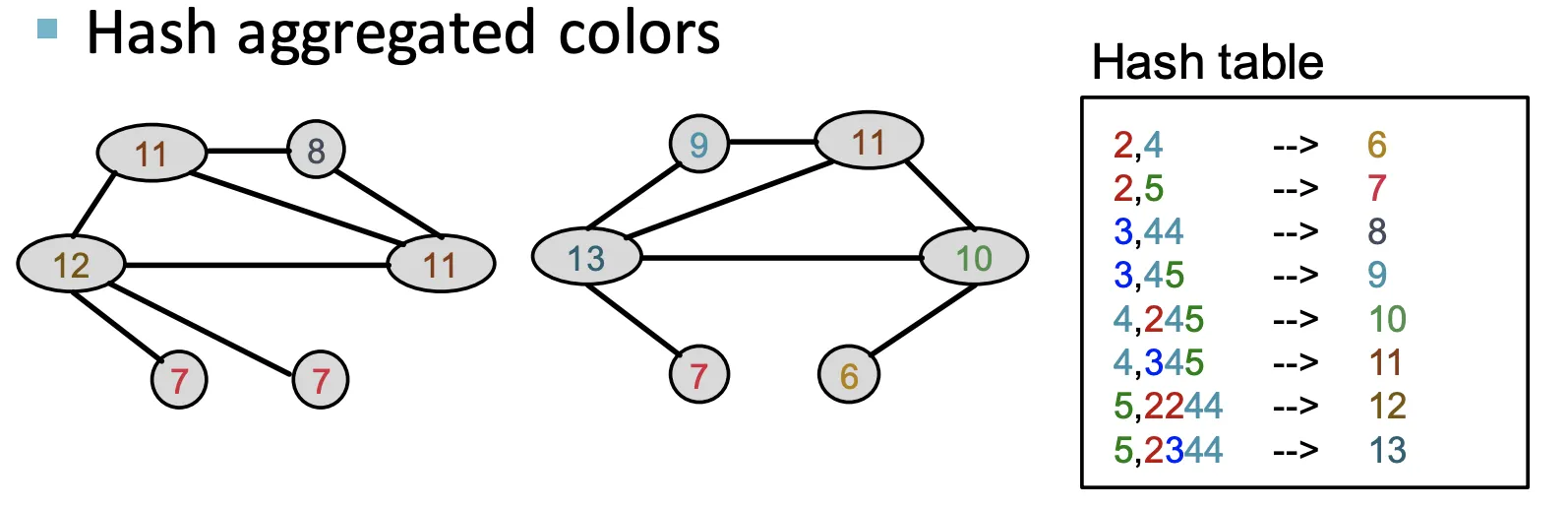
Aggregate된 Color를 HASH한다.
6.
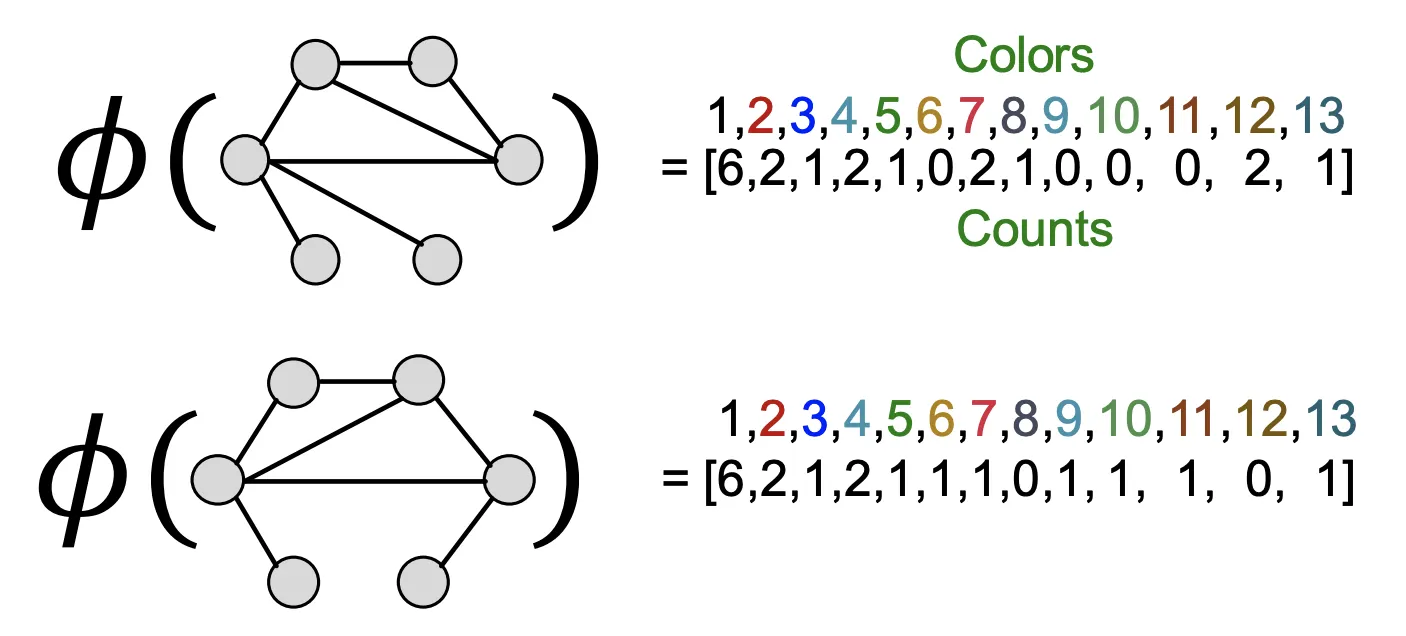
Color Refinement가 끝나면 WL Kernel이 각 Color가 등장했던 횟수를 세서 Summary한다.
7.
Color Count Vector를 내적해 WL Kernel의 결과값을 구한다.
Graph-Level Feature Summary
Graph Level Feature는 Kernel을 이용한다.
1.
Graphlet Kernel :Bag-of-Graphlets, Computationally Expensive
2.
WL- Kernel :
•
Color-Refinement 알고리즘을 이용해 반복적으로 피팅
•
Bag-of-Colors
•
Computationally Efficient !
•
Closely related to Graph Neural Networks