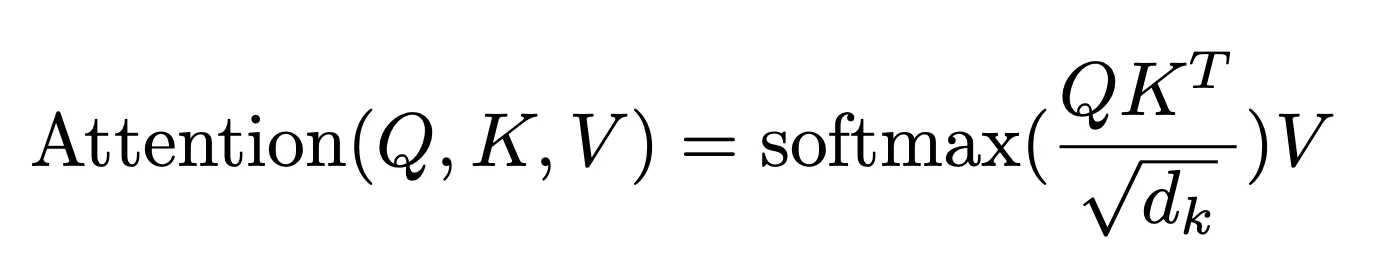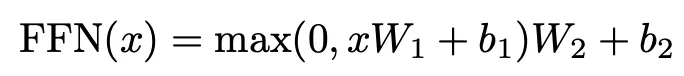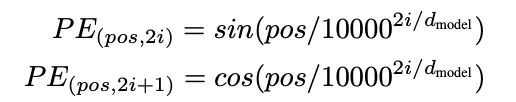2020.08.13
0. Abstract
Sequence 변환 모델은 Encoder - Decoder 구조에 RNNs, CNNs를 기반으로 구축되어 왔습니다.
당대 SOTA모델도 Attention을 추가한 Encoder - Decoder 였는데요,
저자는 Attention을 단독으로 사용한 Transformer라는 구조를 제시합니다.
Transformer는 Sequence 변환 뿐만 아니라 NLP Task 전반에서 획기적인 성능 개선을 가져왔고,
현재까지도 활발하게 응용되고 있습니다. (BERT,GPT,ELECTRA..)
1. Introduction
RNNs
RNNs는 Sequential한 관계를 모델링 하기위해 만들어 졌습니다.
그래서 당연하게도 Sequence에 매우 의존적입니다.
전 시점의 정보를 입력 받아 현재의 입력과 연산해 정보를 추출하고, 또 그걸 다음 시점으로 넘기는 식으로 학습이 이루어집니다.
이런 구조 때문에 본질적으로 병렬 연산을 할 수 없었고,
연산의 비효율성과, Long Term Depedency 문제가 지속적으로 발생하게 됩니다.
Attention
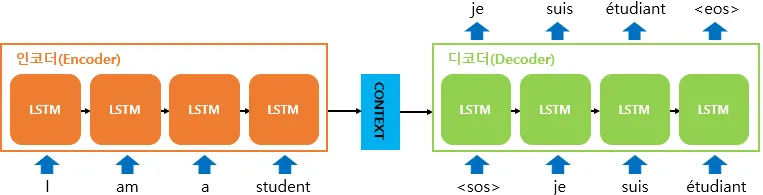
Encoder - Decoder 구조는 기본적으로 Encoder의 마지막 Hidden State를 이용해 Decoder에 정보를 전달합니다.
그 Hidden State를 Context Vector라고 하는데, 이 Vector가 Decoder로 전해지는 Encoder Sequence의 유일한 정보 입니다.
그런데, Context Vector는 결국 고정되어 있는 Vector 이므로 Encoder Sequence의 정보를 충분히 담을 수 없습니다.
따라서 정보의 손실이 발생하게 되고, Sequence가 길어질수록 그 손실이 커지게 됩니다.
저 Context Vector안에 Encoder Sequence의 정보를 다 담기는 어렵습니다.
이를 극복하기 위해 Attention 메커니즘이 고안되었습니다.
Decoder가 고정된 Context Vector 대신 Encoder의 모든 시점을 확인하고
시점의 중요성에 따라 가중치를 두어 정보를 가져오는 것이 Attention의 주요 아이디어 입니다.
이러한 아이디어 덕분에 Sequence 사이의 거리가 멀어도 정보를 전달할 수 있게 되었고
Input과 Output간의 관계(Dependency)를 더 잘 파악할 수 있게 되었습니다.
이러한 장점 때문에 Attention은 RNN이 사용되는 대부분의 Task에 같이 사용되었습니다.
Transformer
Transformer는 기존 Sequence 모델 구조에서 RNN을 제거하고, Attention만 사용하는 구조입니다.
이를 통해 2가지 장점을 얻었고, 두 장점 모두 SOTA 수준을 달성했습니다.
1.
기존 Attention과 같이 Global 하게 Depedency 파악 가능
2.
RNN이 제거 되었으므로 병렬 처리의 효율 극대화
이제 어떻게 RNN을 제거하고, 어떤 구조로 연산이 이루어지는 지를 알아보겠습니다.
2. Model Architecture
대부분의 Sequence 변환 모델은 Encoder - Decoder 구조로 이루어져 있습니다.
•
Encoder :
Symbol Sequence 를 입력 받아
Continous Sequence 으로 매핑합니다.
•
Decoder :
가 주어지면, Decoder는 Symbol Sequnce를 생성합니다.
생성은 한 시점 (Time Step)마다 하나씩 이루어 지고, 생성된 는 다음 시점의 입력으로 사용됩니다.
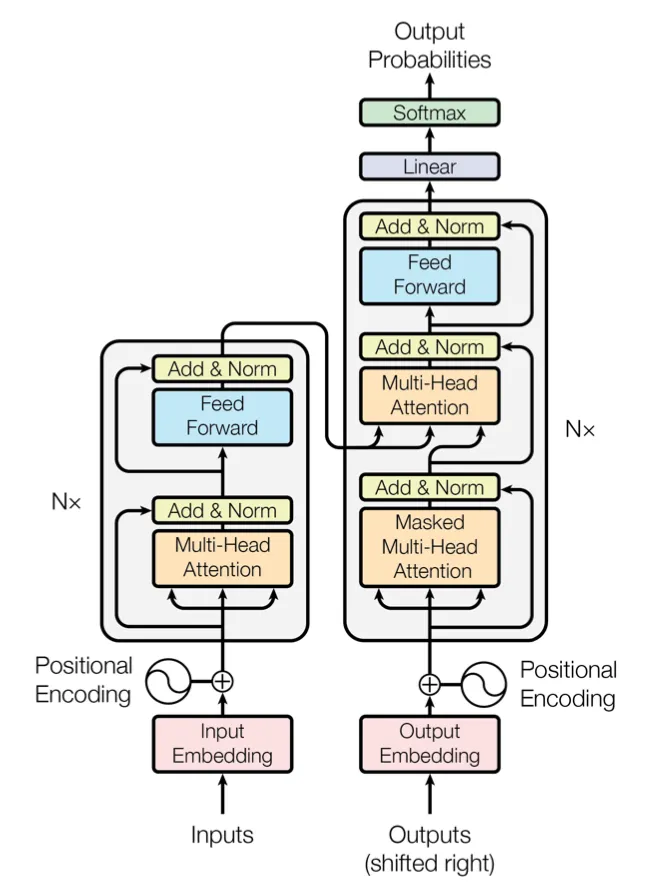
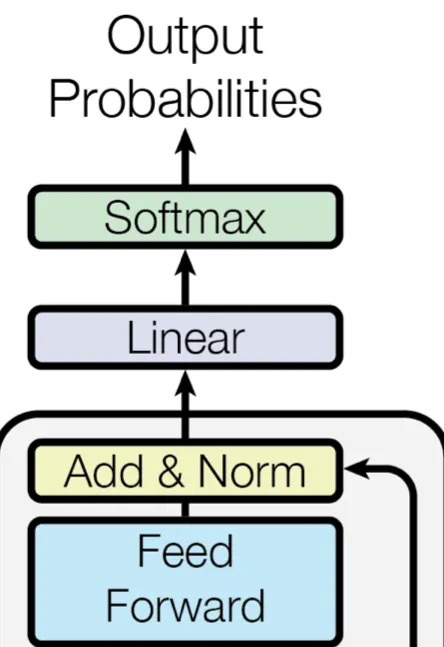
Transformer도 Encoder-Decoder 구조를 띠고 있는데, 요소 Block은 다음과 같습니다.
•
Stacked Self-Attention
•
Point Wise
•
Fully Connected Layers
2.1 Encoder and Decoder Stacks
•
Encoder :
똑같은 Layer를 6개 Stack한 구조입니다 (N=6)
각 Layer는 2개의 Sub Layer로 이루어져 있습니다.
1.
Multi-Head Attention
2.
Position wise fully connected feed-forward network
두 Sub Layer 모두 Residual Connection이 존재하며,
결과값은 LayerNormSublayer 가 됩니다.
용이한 Residual Connection을 위해
Embedding Dim = Output Dim = = 512 로 구성되어 있습니다.
•
Decoder :
똑같은 Layer를 6개 Stack한 구조입니다 (N=6)
대신, 각 Layer가 3개의 Sub Layer로 이루어져 있습니다.
1.
Masked Multi-Head Attention
2.
Multi-Head Attention
3.
Position wise fully connected feed-forward network
Masked Multi-Head Attention은 Self-Attention를 조금 수정한 Layer인데,
Decoder가 다음 단어 예측을 할 때, 미래 시점의 정보가 들어오는 것을 방지하기 위해
미래 시점 값에 대해 모두 Masking을 한 형태입니다.
Residual Connection은 동일한 방식으로 이루어집니다.
[Transformer의 전체적인 구조]
2.2 Attention
우선 기본적인 Encoder - Decoder 구조를 기반으로 Attention을 설명하겠습니다.
Attention의 작동방식을 직관적으로 설명하면 다음과 같습니다
1. 특정 시점의 값이, 다른 모든 시점의 값과 얼마나 연관을 가지고 있는지 계산합니다.
2. 연관성이 높은 시점에 집중해(Attention) 정보를 가져옵니다.
이 과정은 [ Query,
Query,  Keys,
Keys,  Values]간의 연산을 통해 이루어집니다.
Values]간의 연산을 통해 이루어집니다.
{Key : Value}는 Dictionary 처럼 Paring 되어있는 값입니다.
이들의 집합을 Keys와 Values로 부르겠습니다.
Query
- 질문, 다른 시점과의 연관성이 궁금한 시점의 값입니다. (Decoder : )
Keys
- 열쇠, 연관성을 계산해야하는 시점의 값들 입니다. (Encoder :
Values
- 값, 연관성 만큼 가중치를 두어 정보를 가져올 값들 입니다. (Encoder : )
위 비유를 바탕으로, Attention의 실제 작동방식을 설명하면 다음과 같습니다.
1. Decoder의 Hidden Layer인 Query() 와 Encoder의 Hidden Layer인 Keys()를 내적합니다
•
Query는 , Keys는 형태의 벡터입니다. (n = Input Sequence의 길이)
•
Query Keys 를 거치면 형태를 얻습니다.
•
이 벡터는 각 시점에서의 Query와의 연관성을 나타냅니다.
2. Softmax를 이용해, 결과값을 가중치 벡터로 변환합니다.
3. 가중치 벡터를 Encoder의 Hidden Layer 값인 Value와 내적해 Context Vector로 사용합니다.
•
가중치 벡터는 형태의 벡터입니다.
•
Value는 형태의 벡터입니다.
•
Context Vector는 형태의 벡터가 됩니다.
4. Query와 Context Vector를 Concat해 신경망에 흘린뒤 Softmax로 다음 단어를 예측합니다.
•
이 방식을 Additive Attention이라고 합니다.
Transformer는 이 Attention을 그대로 사용하는 것이 아니라, 여러 방식으로 응용해 사용합니다.
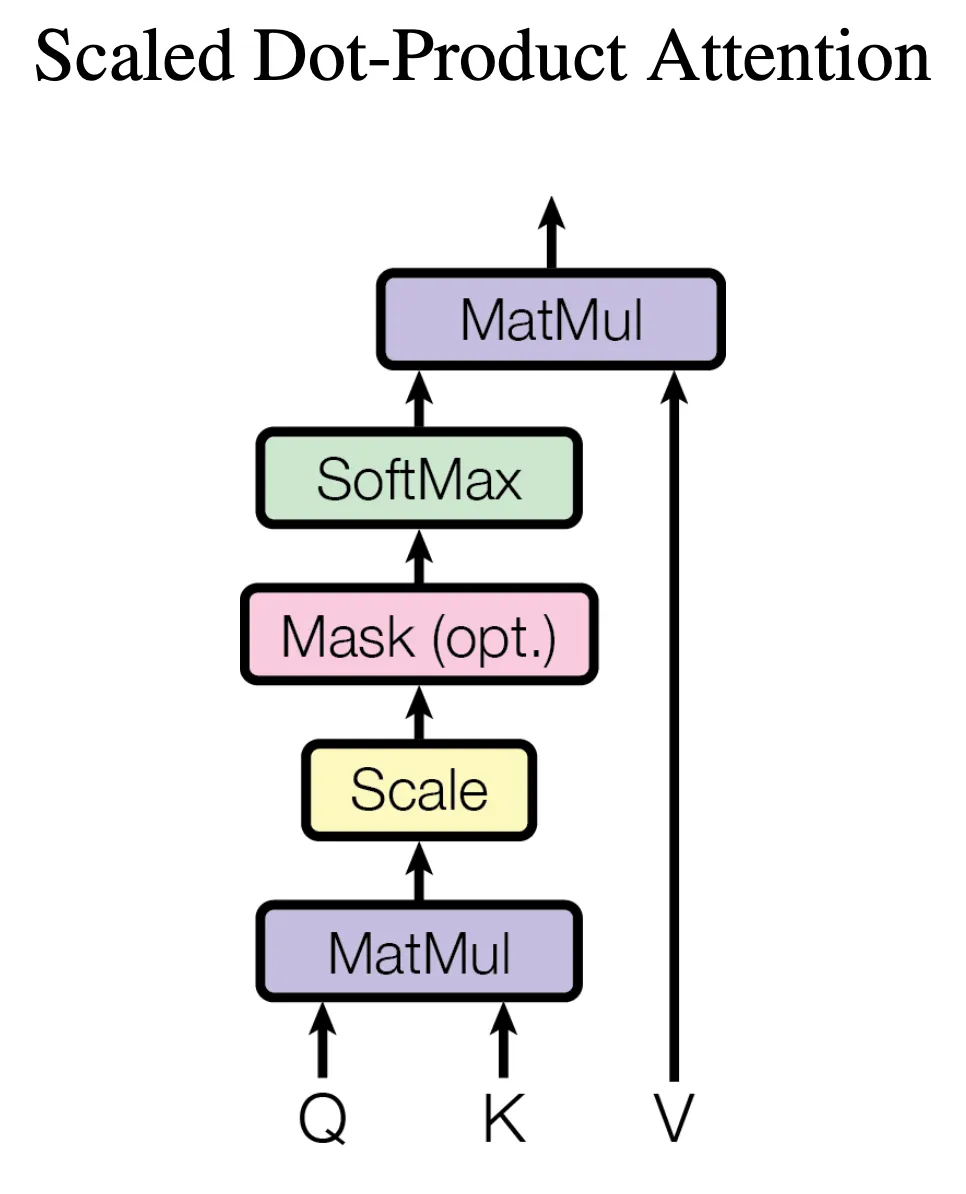
2.2.1 Scaled Dot-Product Attention
Transformer는 Scaled Dot-Product Attention 방식을 통해 Attention 값을 계산합니다.
•
행렬단위로 연산을 진행합니다.
Q : Query 벡터를 묶은 행렬
K : Key 벡터를 묶은 행렬
V : Value 벡터를 묶은 행렬
•
Additive 대신 Dot-Product를 이용합니다.
◦
Attention은 주로 Additive와 Dot-product 방식으로 사용됩니다.
◦
두 방식 모두 시간 복잡도 자체는 비슷하나, 구현체의 존재 때문에 Dot- Product 방식이 빠르고 효율적입니다.
◦
하지만 Dot - Product는 값이 커지면 Softmax값이 극단적으로 나와, Gradient가 죽습니다.
▪
따라서 로 나눠 Scaling을 해줍니다.
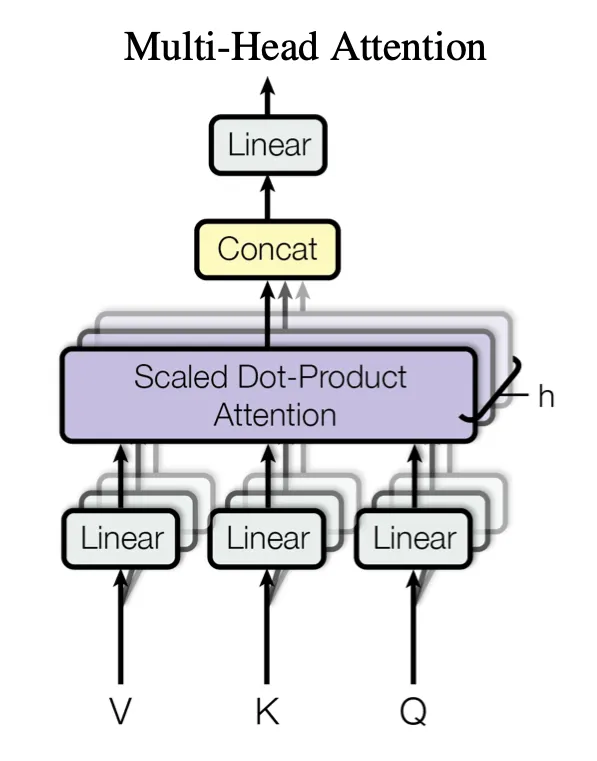
2.2.2 Multi-Head Attention
Transformer는 Attention을 여러 Head로 나누어 병렬적으로 계산합니다.
가중치 차원 설명
•
Multi-Head Attention 이란?
◦
Sinlge-Head Attention은 , 차원의 을 한번에 연산해 Attention을 구합니다.
◦
Transformer에선 이 방법 대신, 차원의 를 개로 나누어 연산하고 각 결과를 Concat해 Attention을 구합니다.
▪
이 방식을 Multi-Head Attention 이라고 부릅니다.
•
연산 과정
1.
에 각 Head의 학습된 가중치인 를 곱합니다
2.
이를 통해 Head 별로 차원의 분할된 행렬을 얻습니다.
3.
Head의 Attention을 병렬적으로 진행합니다.
4.
얻어진 결과를 Concat한뒤, 를 곱해 선형변환을 진행합니다.
5.
그 결과값이 Multi-Head Attention 값이 됩니다.
•
차별점 & 얻는 이점
1.
학습된 가중치를 통해 가 투영 및 분할(Projection) 되는데, 각 가중치가 Head별로 다릅니다.
→ Head마다 다른 기준으로 표현(Representation)을 가져옵니다 → 정보량이 훨씬 풍부해집니다
→ 이후 선형변환이 있어, 그 정보들을 적절히 섞어 사용 가능합니다.
2.
분할된 개의 병렬적인 연산으로 진행됩니다
→ 정보량이 훨씬 풍부함에도 불구하고, 의 Single-Head Attention과 연산비용이 비슷합니다.
•
하이퍼 파라미터
Transformer의 기본 차원() 은 512 이며, Head()는 8개 입니다.
이에 따라 파라미터들을 정리해보면 다음과 같습니다. [ , , ]
2.2.3 Applications of Attention in our Model
Transformer 에서는 3가지 방법으로 Multi-Head attention을 사용합니다.
1.
Encoder - Decoder Attention
•
는 Decoder의 이전 Layer에서 넘어옵니다.
•
는 Encoder의 Output에서 넘어옵니다.
•
이 구조를 통해 Decoder는 Encoder의 모든 시점을 참고할 수 있습니다.
•
이는 전통적인 Seq2Seq의 Attention과 개념이 같습니다.
2.
Encoder의 Self-Attention
•
가 모두 같은 곳에서 넘어옵니다.
•
이 경우 Encoder의 이전 Layer의 결과값이 그 곳이라고 할 수 있습니다.
•
이 구조를 통해 Encoder는 Input Sequence의 모든 시점을 참고할 수 있습니다.
•
즉, Sequence를 구성하는 다른 모든 요소들간의 관계를 파악할 수 있습니다.
3.
Decoder의 Self-Attention
•
Encoder와 거의 유사합니다.
•
한 가지 다른 점은, Decoder의 경우 모든 시점이 아니라 현재 시점까지만 참고할 수 있도록 설계되어 있습니다.
•
이는 다음 시점의 단어를 예측할 때, 다음 시점으로부터 정보가 들어오는 것을 막기 위해서 입니다.
•
이 기능은 Scale Dot-Product Attention Block에 구현되어 있습니다.
[미래 시점의 단어를 로 Masking 합니다]
2.3 Position-wise Feed-Forward Networks
•
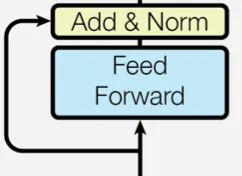
Encoder, Decoder 모두 FC-Feed-Forward Networks(이하FFN)가 존재합니다.
•
각 FFN은 모두 동일한 구조이며, 파라미터는 공유하지 않습니다.
•
2번의 선형 변환과 ReLU 를 이용합니다.
•
Input : 512 → Hidden : 2048 → Output : 512 차원으로 변환됩니다.
2.4 Embeddings and Softmax
•
Transformer도 다른 Sequence Model과 같이 Embedding을 사용합니다.
•
또, Decoder의 Output을 Token으로 변환하기 위해 선형 변환과 Softmax를 사용합니다.
•
즉, 총 3 곳에서 Embedding Matrix의 파라미터가 및 학습 됩니다.
1.
Input Embedding : 입력 Token을 차원의 벡터로 변환합니다
2.
Output Embedding : 입력 Token을 차원의 벡터로 변환합니다
3.
Linear : 입력 표현을 Vocab size 차원의 벡터 즉, 으로 변환합니다
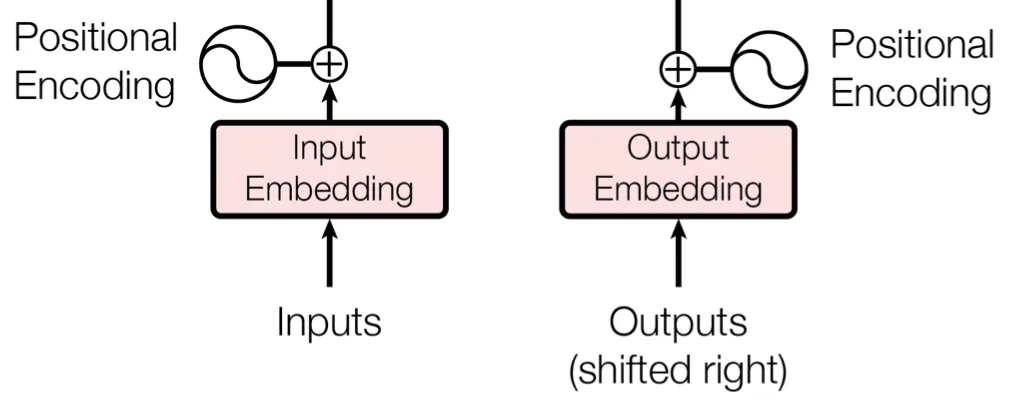
2.5 Positional Encoding
•
Transformer는 Recurrence도, Conv도 포함하고 있지 않습니다.
•
때문에 연산과정에서, Sequence 내에서의 위치 정보를 전달할 수 없습니다.
•
이를 극복하기 위해 Positional Encoding을 사용합니다.
◦
Positional Encoding을 하는 방법은 다양한데, Transformer에선 frequency가 다른 sine,cosine 함수를 사용했습니다.
pos : Position, i = dimension
•
Positional Encoding도 차원의 이므로, Embedding 값과 더해서(sum) 사용됩니다.
3. Why Self-Attention
일반적인 방법들과, Self-Attention 사이의 복잡도 비교
parameters = {
n : '시퀀스의 길이',
d : '표현의 차원',
k : 'CNN 커널의 사이즈',
r : '제한된 Self-Attention의 이웃수',
}
Python
복사
RNN,CNN같이 일반적으로 Sequence 변환에 사용되는 기법 대신 Self-Attention을 사용한 이유는 크게 세 가지 입니다.
1.
Dependency가 걸려있는 단어들의 경로의 길이 문제 (Long - Term Depedency)
Self Attention의 경우가 O(1)의 복잡도로 최대 거리가 가장 짧습니다.
따라서 Self - Attention이 Depedency 파악에 유리합니다.
2. Layer 당 연산 복잡도의 합
n이 d보다 크지 않으면, Self Attention이 유리합니다.
Sequence의 길이가 Dimension보다 큰 구조는 보기 드묾으로, 대부분의 경우 Self - Attention이 연산 면에서 유리합니다.
3. 병렬처리 할 수 있는 최대 연산량 (필요한 Sequential Operation의 최소값으로 측정)
RNN을 제외한 모델들의 최소 Sequential Operation의 복잡도가 O(1)이며, 병렬화가 용이합니다.
4. Training
4 - 1. Training Data and Batching
•
WMT 2014 English-German dataset
◦
450만 문장 쌍을 학습시켰으며, 문장은 Byte-Pair 로 인코딩 시켰습니다.
•
WMT 2014 English-French dataset
◦
3600만 문장 쌍을 학습시켰으며, Word-Piece를 이용해 토큰화 했습니다.
•
Sequence의 길이를 기준으로 batch를 묶었습니다 각 batch는 25000개의 Source Token과, 25000개의 target Token으로 구성되었습니다.
4 - 2. Hardware and Schedule
•
P100 8장으로 학습시켰습니다.
•
논문에 기입된 Hyperparameters로 Base Model을 돌렸을 때 12시간이 걸렸습니다.
•
Big Model을 돌렸을 때, 3.5일이 걸렸습니다.
4 - 3. Optimizer
•
Adam을 이용했으며 로 설정했습니다.
•
lr은 warm up을 이용해 선형 증가, 이후 루트 감소를 의도했습니다.
4 - 4. Regularization
•
Residual DropOut
◦
각 sub-layer에서 Residual Connection이 이루어지기 전 Output에 Dropout을 적용했습니다.
◦
Embedding과 Positional Encoding의 합에도 Dropout을 적용했습니다.
◦
rate는 0.1을 사용했습니다.
•
Label Smoothing
◦
Overconfident를 막기위해 = 0.1 의 Label Smoothing을 사용했습니다.
◦
선택지 개념인 Perplexity는 떨어졌지만, Acc와 BLEU는 상승했습니다.