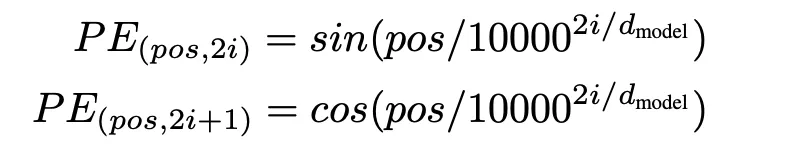0. Positional Encoding 이란
1.
Positional Encoding은 Transformer에서 사용되는 테크닉이다.
2.
Trasnformer의 기본 입력은 Sequence이고, 이를 처리하는 주요 Layer는 Self-Attention이다.
3.
Sequence는 기본적으로 순서에 따른 정보(선후,거리)가 존재한다.
4.
Self-Attention은 RNN과 달리 순서 정보를 내부적으로 모델링 할 수는 구조이다.
5.
Positional Encoding은 이를 극복하기위해 임베딩 벡터에 위치 정보를 더해주는 테크닉이다.
1. Types of Positional Encoding
특정 Sequence에 Position정보를 더해주려면 어떻게 할 수 있을까? Naive한 방법부터 실제 Transofrmer에 사용되는 Sinusoidal 방식까지 살펴보자.
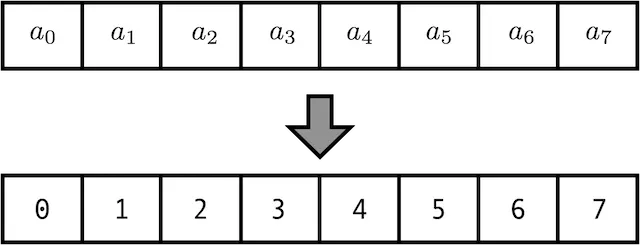
1. Count
방법 : 그냥 Index를 세서 Position으로 넣어준다.
문제 : 일반적으로 Network에 들어가는 Feature대비 Scale이 너무크다. Gradient관련 문제가 생긴다.
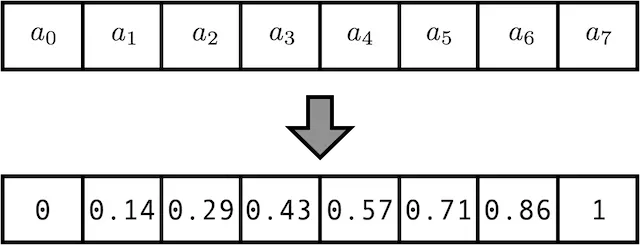
2. Normalized Count
방법 : Count 방법의 문제를 해결하기 위해 가장 큰 값으로 나눈다.
문제 : 가장 큰 값이 길이에 따라 가변적이므로 Position 정보가 매번 바뀐다. 길이가 10인 Sequence의 5번째 위치값이나, 길이가 20인 Sequence의 10번째 위치값이 같다.
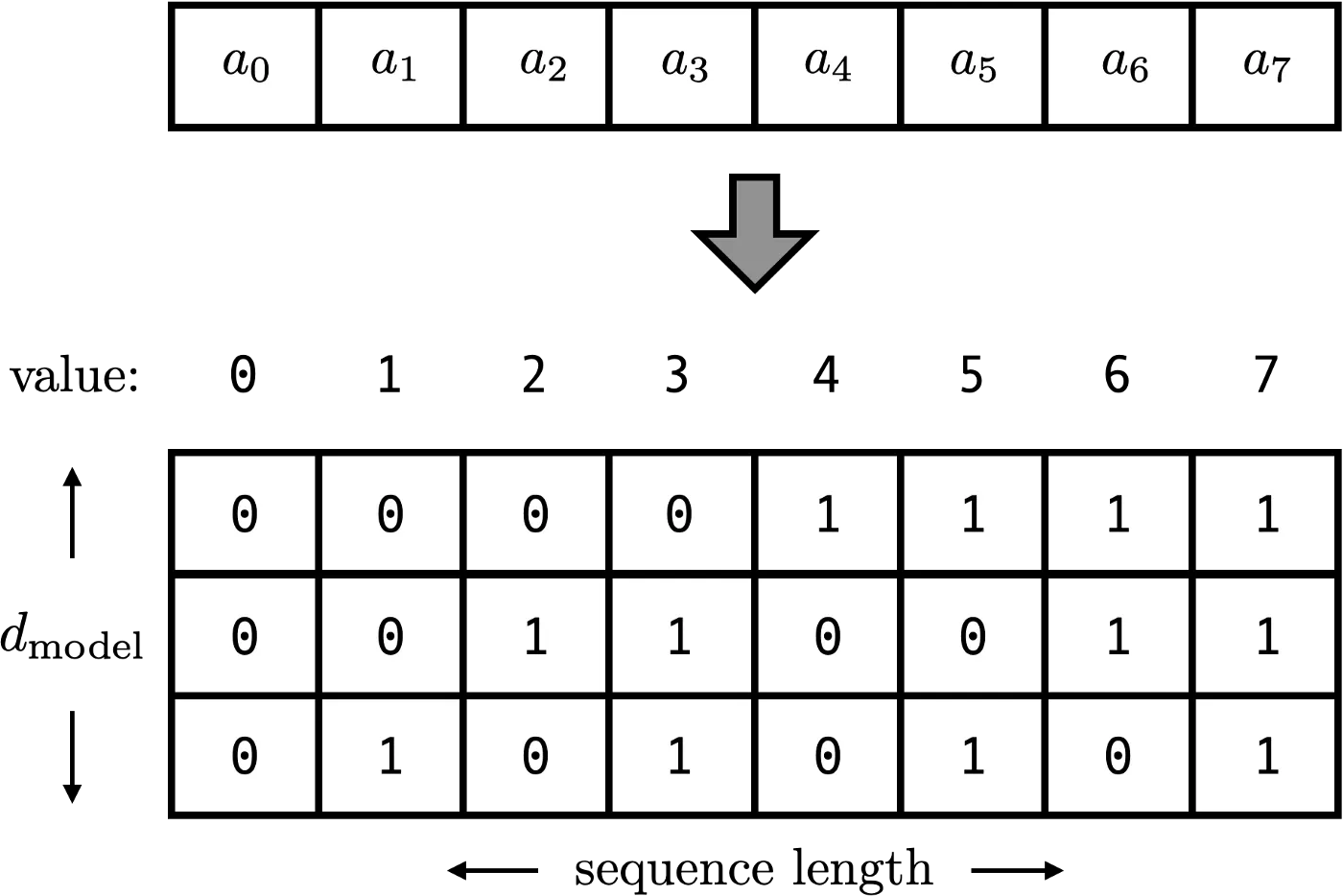
3. Count but Using Binary
방법 : Count하고 결과를 Binary Vector로 표현한다. 값이 0~1에 존재하고, 위치에 따라 고정된 값을 뱉는다.
문제 : Discrete함수의 결과값이라 거리로 사용하기 힘들다
왜 Discrete 하면 거리로 사용하기 힘든가?
4. Continous Binary Vector
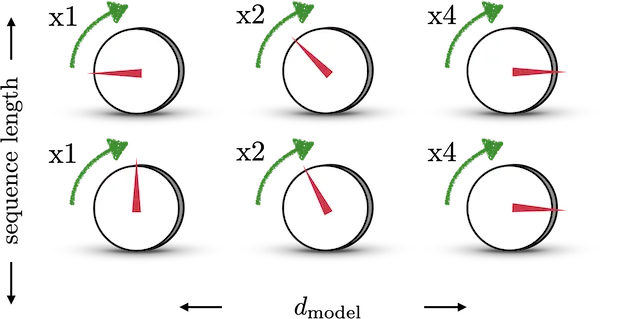
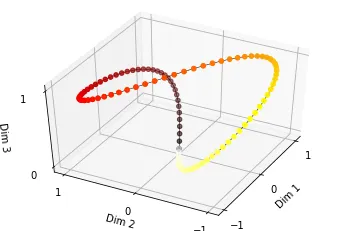
Binary Vector를 Continous하게 만들기 위해선, 그 사이를 주기를 갖고 보간해줄 함수가 필요하다. 이때 삼각함수가 적절한 도구가 될 수 있다. [-1,1]의 범위를 갖고 있으며 주기성또한 존재하기 때문이다. 삼각함수를 적용하기 위한 설명을 위해 아래 그림을 보자.
왼쪽 그림의 각 다이얼은 에 따라 다른속도로 돌고 있으며, 배수는 90도 회전을위해 걸리는 TimeStep을 의미한다. 우측으로 한 칸 갈수록 같은 회전에 걸리는 시간이 2배가 된다. 이를 식으로 표현하면 로 표현이 가능하다. 우측 그림은 이렇게 만들어진 Position 정보를 시각화 한 그림인데, 각 Step 마다 거리가 일정한 함수가 되었다.
그러나 아직 고쳐야 할 문제점이 남아있다.
문제 1 : 주기가 서로 얽혀있어(으로 처음 Index로 돌아가는 구조로 되어있다. 이러면 첫 인덱스와 멀리 떨어진 인덱스가 동일한 Position을 갖게된다.
해결 : 굳이 주기를 으로 Binary하게 설정하지 않아도 된다. 따라서 주기를 로 변경한다
문제 2 : 특정 Position을 다른 Position의 함수로 표현할 수 없다.
해결 : cosine을 사용한다.
해결책을 넣은 결과물은 Transformer에서 사용중인 Sinusoidal Positional Encoding과 같다.