Home
///
///
📌

Back to the Basic: Deep Learning Optimizer

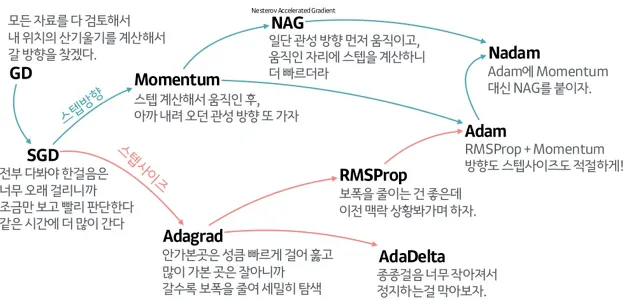
출처 : https://www.slideshare.net/yongho/ss-79607172 
Saddle Point에서 각각의 Optimizer가 작동하는 방식

0. Motivation

이전 글에서 Gradient Descent를 알아봤다. Gradient Descent는 사실 저것만으로 잘 작동하지 않는다. Local Minimum & Saddle Point 문제 때문이다. Linear Model에선 Gradient가 0이 되는 지점이 하나뿐이었지만, 문제와 모델이 복잡해지면 Cost 함수의 곡선도 복잡해지면서 최저점이 아님에도 Gradient가 0이 되는 지점이 많이 생긴다. Local Minimum처럼 국소적인 최저점이 될 수도 있고, Saddle Point처럼 최저점도 아닌데 평평한 될 수도 있다. 이론적으로 SGD, M-BSGD 만으로는 이런 지점을 빠져나오기 힘들다.(실제로는 Gradient가 Noisy해서 운좋게 나올때도 있지만) 이를 극복하기 위해 여러 Optimizer가 개발되었다.

1. Momentum

말 그대로 관성을 이용한 Optimizer이다. 직관적으로 생각해서 국소적으로 평평한 지점에서 멈추는게 문제라면, 관성을 붙여서 빠져나가게 하면 되는 것이다. 이를 위해 이전 Gradient가 얼마였는지를 이용한다. Momentum은 (1) One Side한 Gradient의 경우 점점 가속도를 붙여 최적화를 빠르게 만들어주고, (2) Local Minimum이나 Saddle Point같이 최저점이 아닌데 평평해서 Gradient가 작아지는 구간을 탈출할 수 있도록 도와준다.
Momentum은 t시점의 업데이트 할 가중치를 다음과 같은 수식으로 구한다.
1.
Vt=m∗Vt−1−η∇θJ(θ)V_t = m *V_{t-1} - \eta \nabla_\theta J(\theta) (mm은 관성 계수이며, 일반적으로 0.9)
2.
θ=θ+Vt\theta = \theta + V_t

2. NAG

NAG는 Nesterov Accelerated Gradient의 줄임말로 Nestreov가 만든 Momentum의 변종이다. 일반적으로 Momentum보다 더 빠르다고 알려져있다. 기본적인 아이디어는 Momentum을 이용해 Gradient를 예측 계산하는 것이다. 즉 Momentum Vetector VtV_t 방향으로 미리 이동시킨 다음 Gradient를 계산한다.
(1) Momentum Vector VtV_{t}가 가르키는 방향이 최저점 방향이라면 Momentum 보다 최적화가 빠르고 (2) 최저점에 도달했음에도 Momentum 때문에 진동하면서 수렴을 못하는 현상을 막아준다.
수식으로 표현하면 다음과 같다
1.
Vt=m∗Vt−1−η∇θJ(θ+m∗Vt−1)V_t = m *V_{t-1} - \eta \nabla_\theta J(\theta + m*V_{t-1})
2.
θ=θ+Vt\theta= \theta + V_t

3. Adagrad

Adagrad 는 Adaptive하게 Gradient를 조정한다는 뜻이다. Gradient가 가팔라서, 많이 Update된 차원의 Gradient를 임의적으로 줄이는 방식이다. Learning Rate가 점점 작아지는 것과 같으며, 이런 조정은 결국 Gradient가 Global Minimum 방향을 가르키도록 유도하는 역할을 한다. 다만 딥러닝을 할때 사용하면 Learning Rate가 너무 빨리 줄어들어서 Gradient가 사라져버린다.
수식으로 표현하면 다음과 같다.
1.
st=st−1+η∇θJ(θ)⊗η∇θJ(θ)s_t = s_{t-1} + \eta \nabla_\theta J(\theta) \otimes \eta \nabla_\theta J(\theta)
2.
θ=θ−η∇θJ(θ)⊘s+ϵ\theta = \theta - \eta \nabla_\theta J(\theta) \oslash \sqrt{s+\epsilon} (ϵ\epsilon은 0으로 나누는걸 막기 위한 값으로 일반적으로 1e-9)
풀어서 설명하면 (1) sts_t에 Gradient의 제곱을 누적시킨다. (2) Gradient에 s\sqrt{s}를 나눠주어서 Gradient를 줄이는데, 기존에 Gradient가 큰 차원은 크게 감소하고, 작은 차원은 조금 감소한다.

4. RMSProp

Adagrad는 설명했듯이 너무 빨리 Gradient가 사라져버린다. 그 이유중 하나는 tt가 진행됨에 따라 s s가 누적되어분모가 점점 커지기 때문인데, RMSProp은 최근의 Gradient에 큰 가중치를 두고, 이전 Gradient의 영향을 줄여서 이 문제를 해결한다. 이전의 영향을 줄여주었을 지수적으로 줄여주었을 뿐인데, AdaGrad보다 훨씬 잘 작동해서 이후 설명할 Adam 이전까진 지배적인 Optimizer였다.
수식으로 표현하면 다음과 같다.
1.
st=β∗st−1+(1−β)×(η∇θJ(θ)⊗η∇θJ(θ))s_t =\beta * s_{t-1} + (1-\beta) \times(\eta \nabla_\theta J(\theta) \otimes \eta \nabla_\theta J(\theta)) (β\beta는 Decay Rate로 일반적으로 0.9)
2.
θ=θ−η∇θJ(θ)⊘s+ϵ\theta = \theta - \eta \nabla_\theta J(\theta) \oslash \sqrt{s+\epsilon}

5. Adam

Adam은 Adaptive + Momentum이라는 뜻이다. RMSProp에 Momentum을 합친 Optimizer다. 가장 광범위하게 Baseline으로 쓰이는 Optimizer이다. 수식으로 표현하면 다음과 같으며 1번이 Momentum, 2번이 RMSProp과 유사하다.
1.
Vt=β1Vt−1−(1−β1)∇θJ(θ)V_t = \beta_1V_{t-1} - (1-\beta_1) \nabla_{\theta}J(\theta) (β1\beta_1은 1st Momentum, 일반적으로 0.9)
2.
st=β2st−1+(1−β2)∇θJ(θ)⊗∇θJ(θ)s_t =\beta_2s_{t-1}+(1-\beta_2) \nabla_\theta J(\theta) \otimes \nabla_\theta J(\theta) (β2\beta_2는 2st Momentum, 일반적으로 0.999)
3.
V^t=Vt1−β1t\hat V_t = {V_t\over1-{\beta_1}^t}
4.
s^t=st1−β2t\hat s_t = {s_t\over1-{\beta_2}^t}
5.
θ=θ+ηm^⊘(s^+ϵ)\theta = \theta + \eta \hat m \oslash \sqrt{(\hat s+\epsilon)}